Download P - UCL

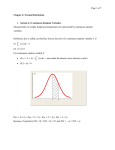
Statistics for variationists
- or what a linguist needs to know about statistics
Sean Wallis
Survey of English Usage
University College London
[email protected]
Outline
• What is the point of statistics?
– Variationist corpus linguistics
– How inferential statistics works
• Introducing z tests
– Two types (single-sample and two-sample)
– How these tests are related to χ²
• ‘Effect size’ and comparing results of
experiments
• Methodological implications for corpus
linguistics
What is the point of statistics?
• Analyse data you already have
– corpus linguistics
• Design new experiments
– collect new data, add annotation
– experimental linguistics ‘in the lab’
• Try new methods
– pose the right question
• We are going to focus on
z and χ² tests
What is the point of statistics?
• Analyse data you already have
– corpus linguistics
• Design new experiments
– collect new data, add annotation
– experimental linguistics ‘in the lab’
• Try new methods
– pose the right question
• We are going to focus on
z and χ² tests
}
observational
science
}
}
}
experimental
science
philosophy of
science
a little maths
What is ‘inferential statistics’?
• Suppose we carry out an experiment
– We toss a coin 10 times and get 5 heads
– How confident are we in the results?
• Suppose we repeat the experiment
• Will we get the same result again?
• Inferential statistics is a method of inferring
the behaviour of future ‘ghost’ experiments
from one experiment
– We infer from the sample to the population
• Let us consider one type of experiment
– Linguistic alternation experiments
Alternation experiments
• A variationist corpus paradigm
• Imagine a speaker forming a sentence as a
series of decisions/choices. They can
– add: choose to extend a phrase or clause, or stop
– select: choose between constructions
• Choices will be constrained
– grammatically
– semantically
Alternation experiments
• A variationist corpus paradigm
• Imagine a speaker forming a sentence as a
series of decisions/choices. They can
– add: choose to extend a phrase or clause, or stop
– select: choose between constructions
• Choices will be constrained
– grammatically
– semantically
• Research question:
– within these constraints,
what factors influence the particular choice?
Alternation experiments
• Laboratory experiment (cued)
– pose the choice to subjects
– observe the one they make
– manipulate different potential influences
• Observational experiment (uncued)
– observe the choices speakers make when they
make them (e.g. in a corpus)
– extract data for different potential influences
• sociolinguistic: subdivide data by genre, etc
• lexical/grammatical: subdivide data by elements in
surrounding context
– BUT the alternate choice is counterfactual
Statistical assumptions
A random sample taken from the population
– Not always easy to achieve
• multiple cases from the same text and speakers, etc
• may be limited historical data available
– Be careful with data concentrated in a few texts
The sample is tiny compared to the population
– This is easy to satisfy in linguistics!
Observations are free to vary (alternate)
Repeated sampling tends to form a Binomial
distribution around the expected mean
– This requires slightly more explanation...
The Binomial distribution
• Repeated sampling tends to form a Binomial
distribution around the expected mean P
F
• We toss a coin
10 times, and
get 5 heads
N=1
P
x
1
3
5
7
9
The Binomial distribution
• Repeated sampling tends to form a Binomial
distribution around the expected mean P
F
• Due to chance,
some samples
will have a
higher or lower
score
N=4
P
x
1
3
5
7
9
The Binomial distribution
• Repeated sampling tends to form a Binomial
distribution around the expected mean P
F
• Due to chance,
some samples
will have a
higher or lower
score
N=8
P
x
1
3
5
7
9
The Binomial distribution
• Repeated sampling tends to form a Binomial
distribution around the expected mean P
F
• Due to chance,
some samples
will have a
higher or lower
score
N = 12
P
x
1
3
5
7
9
The Binomial distribution
• Repeated sampling tends to form a Binomial
distribution around the expected mean P
F
• Due to chance,
some samples
will have a
higher or lower
score
N = 16
P
x
1
3
5
7
9
The Binomial distribution
• Repeated sampling tends to form a Binomial
distribution around the expected mean P
F
• Due to chance,
some samples
will have a
higher or lower
score
N = 20
P
x
1
3
5
7
9
The Binomial distribution
• Repeated sampling tends to form a Binomial
distribution around the expected mean P
F
• Due to chance,
some samples
will have a
higher or lower
score
N = 24
P
x
1
3
5
7
9
Binomial  Normal
• The Binomial (discrete) distribution is close to
the Normal (continuous) distribution
F
x
1
3
5
7
9
The central limit theorem
• Any Normal distribution can be defined by
only two variables and the Normal function z
F
 population
mean P
 standard deviation
s =  P(1 – P) / n
z.s
0.1
0.3
– With more
data in the
experiment, s
will be smaller
z.s
0.5
0.7
p
– Divide x by 10
for probability
scale
The central limit theorem
• Any Normal distribution can be defined by
only two variables and the Normal function z
F
 population
mean P
 standard deviation
s =  P(1 – P) / n
z.s
z.s
– 95% of the curve is within ~2 standard
deviations of the expected mean
2.5%
2.5%
– the correct figure
is 1.95996!
95%
0.1
0.3
0.5
0.7
p
= the critical value
of z for an error
level of 0.05.
The central limit theorem
• Any Normal distribution can be defined by
only two variables and the Normal function z
F
 population
mean P
 standard deviation
s =  P(1 – P) / n
z.s
z.s
2.5%
za/2
= the critical value
of z for an error
level a of 0.05.
2.5%
95%
0.1
0.3
0.5
0.7
p
The single-sample z test...
• Is an observation p > z standard deviations
from the expected (population) mean P?
F
observation p
z.s
0.25%
0.1
z.s
0.25%
P
0.3
0.5
• If yes, p is
significantly
different
from P
0.7
p
...gives us a “confidence interval”
• P ± z . s is the confidence interval for P
– We want to plot the interval about p
F
z.s
0.25%
0.1
z.s
0.25%
P
0.3
0.5
0.7
p
...gives us a “confidence interval”
• P ± z . s is the confidence interval for P
– We want to plot the interval about p
observation p
F
w– w+
P
0.25%
0.1
0.3
0.5
0.25%
0.7
p
...gives us a “confidence interval”
• The interval about p is called the
Wilson score interval
• This interval is
asymmetric
• It reflects the
Normal interval
about P:
observation p
F
w– w+
P
0.25%
0.1
0.3
0.5
0.25%
0.7
• If P is at the upper
limit of p,
p is at the lower
limit of P
(Wallis, to appear, a)
p
...gives us a “confidence interval”
• The interval about p is called the
Wilson score interval
• To calculate w–
and w+ we use
this formula:
observation p
F
z2
p
z
2n
w– w+
P
0.25%
0.1
0.3
0.5
0.25%
0.7
p(1  p) z 2
 2
n
4n
z2
1
n
(Wilson, 1927)
p
Plotting confidence intervals
• Plotting modal shall/will over time (DCPSE)
1.0
p(shall | {shall, will})
• Highly skewed p
in some cases
0.8
–
0.6
p = 0 or 1
(circled)
• Confidence
intervals identify
the degree of
certainty in our
results
0.4
0.2
0.0
1955
• Small amounts of
data / year
1960
1965
1970
1975
1980
1985
1990
1995
(Wallis, to appear, a)
Plotting confidence intervals
• Probability of adding successive attributive
adjective phrases (AJPs) to a NP in ICE-GB
– x = number of AJPs
0.25
• NPs get longer
 adding AJPs is
more difficult
p
0.20
0.15
• The first two falls
are significant,
the last is not
0.10
0.05
x
0.00
0
1
2
3
4
2 x 1 goodness of fit χ² test
• Same as single-sample z test for P (z² = χ²)
– Does the value of a affect p(b)?
F
p(b | a)
z.s
z.s
p(b)
P = p(b)
p(b | a)
p
IV: A = {a, ¬a}
DV: B = {b, ¬b}
2 x 1 goodness of fit χ² test
• Same as single-sample z test for P (z² = χ²)
• Or Wilson test for p (by inversion)
F
P = p(b)
w+
p(b)
w–
p(b | a)
p(b | a)
p
IV: A = {a, ¬a}
DV: B = {b, ¬b}
The single-sample z test
• Compares an observation with a given value
– Compare p(b | a) with p(b)
– A “goodness of fit” test
– Identical to a standard 21 χ² test
• Note that p(b) is given
– All of the variation is assumed
to be in the estimate of p(b | a)
– Could also compare
p(b | ¬a) with p(b)
p(b)
p(b | a)
p(b | ¬a)
z test for 2 independent proportions
• Method: combine observed values
– take the difference (subtract) |p1 – p2|
– calculate an ‘averaged’ confidence interval
F
p2 = p(b | ¬a)
O1
O2
p1 = p(b | a)
(Wallis, to appear, b)
p
z test for 2 independent proportions
• New confidence interval D = |O1 – O2|
^
^
– standard deviation s' = p(1
– p)
(1/n1 +1/n2)
– p^ = p(b)
– compare
x
z.s' with
D
x = |p1 – p2|
z.s'
mean x = 0
p
0
(Wallis, to appear, b)
z test for 2 independent proportions
• Identical to a standard 22 χ² test
– So you can use the usual method!
z test for 2 independent proportions
• Identical to a standard 22 χ² test
– So you can use the usual method!
• BUT: 21 and 22 tests have different purposes
– 21 goodness of fit compares
single value a with superset A
A
• assumes only a varies
– 22 test compares two values
a, ¬a within a set A
• both values may vary
a
¬a
2  2 c2
IV: A = {a, ¬a}
z test for 2 independent proportions
• Identical to a standard 22 χ² test
– So you can use the usual method!
• BUT: 21 and 22 tests have different purposes
– 21 goodness of fit compares
single value a with superset A
A
• assumes only a varies
– 22 test compares two values
a, ¬a within a set A
• both values may vary
• Q: Do we need χ²?
a
¬a
2  2 c2
IV: A = {a, ¬a}
Larger χ² tests
• χ² is popular because it can be applied to
contingency tables with many values
• r  1 goodness of fit χ² tests (r  2)
• r  c χ² tests for homogeneity (r,c  2)
• z tests have 1 degree of freedom
• strength: significance is due to only one source
• strength: easy to plot values and confidence intervals
• weakness: multiple values may be unavoidable
• With larger χ² tests, evaluate and simplify:
• Examine χ² contributions for each row or column
• Focus on alternation - try to test for a speaker choice
How big is the effect?
• These tests do not measure the strength of
the interaction between two variables
– They test whether the strength of an interaction is
greater than would be expected by chance
• With lots of data, a tiny change would be significant
• Don’t use χ², p or z values to compare two
different experiments
– A result significant at p<0.01 is not ‘better’ than
one significant at p<0.05
• There are a number of ways of measuring
‘association strength’ or ‘effect size’
How big is the effect?
• Percentage swing
– swing d = p(a | ¬b) – p(a | b)
– % swing d % = d/p(a | b)
– frequently used (“X increased by 50%”)
• may have confidence intervals on change
• can be misleading (“+50%” then “-50%” is not zero)
– one change, not sequence
– over one value, not multiple values
How big is the effect?
• Percentage swing
– swing d = p(a | ¬b) – p(a | b)
– % swing d % = d/p(a | b)
– frequently used (“X increased by 50%”)
• may have confidence intervals on change
• can be misleading (“+50%” then “-50%” is not zero)
– one change, not sequence
– over one value, not multiple values
• Cramér’s φ
–  =  χ²/N
– c =  χ²/(k – 1)N
(22) N = grand total
(r c ) k = min(r, c)
• measures degree of association of one variable with
another (across all values)
Comparing experimental results
• Suppose we have two similar experiments
– How do we test if one result is significantly
stronger than another?
Comparing experimental results
• Suppose we have two similar experiments
– How do we test if one result is significantly
stronger than another?
• Test swings
– z test for two samples from different populations
0
– Use s' =  s12 + s22
-0.1
– Test |d1(a) – d2(a)| > z.s' -0.2
-0.3
-0.4
-0.5
-0.6
-0.7
d1(a)
d2(a)
(Wallis 2011)
Comparing experimental results
• Suppose we have two similar experiments
– How do we test if one result is significantly
stronger than another?
• Test swings
– z test for two samples from different populations
0
– Use s' =  s12 + s22
-0.1
– Test |d1(a) – d2(a)| > z.s' -0.2
• Same method can be
used to compare
other z or χ² tests
-0.3
-0.4
-0.5
-0.6
-0.7
d1(a)
d2(a)
(Wallis 2011)
Modern improvements on z and χ²
• ‘Continuity correction’ for small n
– Yates’ χ2 test
– errs on side of caution
– can also be applied to Wilson interval
• Newcombe (1998) improves on 22 χ² test
– combines two Wilson score intervals
– performs better than χ² and log-likelihood (etc.)
for low-frequency events or small samples
• However, for corpus linguists, there remains
one outstanding problem...
Experimental design
• Each observation should be free to vary
– i.e. p can be any value from 0 to 1
p(b | words)
p(b | VPs)
p(b | tensed VPs)
b1
b2
Experimental design
• Each observation should be free to vary
– i.e. p can be any value from 0 to 1
• However many people use
these methods incorrectly
– e.g. citation ‘per million words’
• what does this actually mean?
p(b | words)
p(b | VPs)
p(b | tensed VPs)
b1
b2
Experimental design
• Each observation should be free to vary
– i.e. p can be any value from 0 to 1
• However many people use
these methods incorrectly
– e.g. citation ‘per million words’
• what does this actually mean?
p(b | words)
p(b | VPs)
p(b | tensed VPs)
• Baseline should be choice
– Experimentalists can design
b1
b2
choice into experiment
– Corpus linguists have to infer when speakers had
opportunity to choose, counterfactually
A methodological progression
• Aim:
– investigate change when speakers have a choice
• Four levels of experimental refinement:

pmw
words
A methodological progression
• Aim:
– investigate change when speakers have a choice
• Four levels of experimental refinement:


pmw
select a
plausible
baseline
words
tensed VPs
A methodological progression
• Aim:
– investigate change when speakers have a choice
• Four levels of experimental refinement:



pmw
select a
plausible
baseline
grammatically
restrict data or
enumerate cases
words
tensed VPs
{will, shall}
A methodological progression
• Aim:
– investigate change when speakers have a choice
• Four levels of experimental refinement:




pmw
select a
plausible
baseline
grammatically
restrict data or
enumerate cases
check each case
individually for
plausibility of
alternation
words
tensed VPs
{will, shall}
{will, shall}
Ye shall be saved
Conclusions
• The basic idea of these methods is
– Predict future results if experiment were repeated
• ‘Significant’ = effect > 0 (e.g. 19 times out of 20)
• Based on the Binomial distribution
– Approximated by Normal distribution – many uses
• Plotting confidence intervals
• Use goodness of fit or single-sample z tests to compare an
observation with an expected baseline
• Use 22 tests or two independent sample z tests to compare two
observed samples
• When using larger r c tests, simplify as far as possible to
identify the source of variation!
• Take care with small samples / low frequencies
– Use Wilson and Newcombe’s methods instead!
Conclusions
• Two methods for measuring the ‘size’ of an experimental
effect
– absolute or percentage swing
– Cramér’s φ
• You can compare two experiments
• These methods all presume that
– observed p is free to vary (speaker is free to choose)
• If this is not the case then
– statistical model is undermined
• confidence intervals are too conservative
– but multiple changes are combined into one
• e.g. VPs increase while modals decrease
• so significant change may not mean what you think!
References
•
•
•
•
Newcombe, R.G. 1998. Interval estimation for the difference between
independent proportions: comparison of eleven methods.
Statistics in Medicine 17: 873-890
Wallis, S.A. 2011. Comparing χ² tests for separability.
London: Survey of English Usage, UCL
Wallis, S.A. to appear, a. Binomial confidence intervals and contingency
tests. Journal of Quantitative Linguistics
Wallis, S.A. to appear, b. z-squared: The origin and use of χ².
Journal of Quantitative Linguistics
•
Wilson, E.B. 1927. Probable inference, the law of succession, and
statistical inference. Journal of the American Statistical Association 22:
209-212
•
NOTE: My statistics papers, more explanation, spreadsheets etc. are
published on corp.ling.stats blog: http://corplingstats.wordpress.com