* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download None of the above!!
Survey
Document related concepts
Transcript
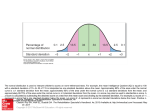
Why stats in psych? Student notes Fill in the blanks on your slides as I proceed through the lecture! 1. Stats allow psychologists to make sense of their data and draw more ____________________ than _______________ observations would provide 2. They create an ____________, ___________ way to prove whether a set of data from an experiment presents us with significant or insignificant results 3. They help psychologists determine if their ______________ was correct or incorrect Descriptive Statistics Descriptive statistics: Describe the qualities of a set of data 1. __________________ a) Is there a _________________________ between 2 factors? Does the presence or absence of 1 thing predict the presence or absence of the other? 2. Measurement of ____________________ a) How common/frequent was a given score? b) What was the __________ performance for the group? c) How might the data be __________ by an unusually high or low score (________)? 3. Measure of _________________ a) By how much do the scores in a data set vary from the average (mean)? b) How big is the _____________ of scores (what is the difference between the lowest and highest score?) c) How can I compare scores from 2 different distributions? ________________ Inferential Statistics Inferential statistics: Tell whether data can be applied to general population (e.g. “What can we infer about human behavior or mental processes in general based on the data from this study?”) 1. Measure of _____________________ a) Does the data allow us to make conclusions related to the hypothesis? b) How certain are we that the data proves the hypothesis rather than just being coincidence or chance results? Big dog to remember with inferential stats :______________! Descriptive Stats Part 1 Correlations: Fill in the blanks in the statements. 1. ______________________: number between -1 and +1 indicates the ___________ of the correlation between 2 variables (coefficient of 0 means _______________!) 2. Correlation graphs are called: ____________________ 3. Line of best fit (AKA ______________ ) drawn near and in direction of majority of dots on graph 4. Upward sloping = ___________ correlation (correlation coefficient between +0.1 and +1) the presence or increase of one indicates the presence or increase of the other 5. Downward sloping = ____________ correlation (correlation coefficient between -0.1 and -1) • the presence or increase of one indicates the absence or decrease of the other 6. Describe the correlations you see in graphs the 3 below using the following terms: weak, strong, or perfect none, negative or positive Descriptive Stats Part 2 Measurements of Central Tendency: Mean, mode, and median A. ________: most frequently occurring # in a set of data B. __________: “average”-- sum of all values divided by total # of values in a set of data C. _________: the middle value in a range of data when data is lined up from lowest value to highest—half of the data are higher in value and half are lower in value than the median Inferential Stats ____________( _______ is the magic number! It means we can say we are 95% sure the results were NOT just a matter of chance.) • • • Scientists have chosen a p value of 0.05 as the maximum p value to be able to say results of a study are statistically significant rather than due to chance p values must be greater than 0 and smaller than 1. The smaller the p value, the more we can say that random chance did NOT create the results You do NOT need to know how to calculate a p value; just remember the magic number and what it means Questions we might ask about John’s experiment to determine if his results were just a result of chance: a)Is 20 participants really enough for him to draw a conclusion? What might be a better sample size for this type of study? b)Is a 4 second difference between the means of the females and males statistically significant for this kind of task? –As a ratio of the total time on average, 4 seconds is approximately 7%. –If the task had taken 24 hours on average, 4 seconds difference would probably be considered statistically insignificant! Descriptive Stats Part 3: Standard deviation and z scores! A better way to compare classes than looking at the mean To put it simply, standard of deviation states the average distance away from __________ that the other scores fall a) A large standard deviation means the spread/range of data is large b) A small standard deviation means the scores (data) are all bunched near the mean c) If you want data that is statistically significant, a SMALL standard deviation is what you want!! d) How are standard deviation and p value related? •Small standard deviation (derived in descriptive stats) is used to determine low p value (part of inferential stats!!) a)___________: a way to compare data in units of standard deviation a) can be negative (means score falls to left of the mean on a graph) b) can be positive (score falls to right of the mean on a graph) John’s Experiment John runs an experiment in which he is recording how long (in seconds) it takes each male and female participant to sort shapes into a Venn diagram. His hypothesis is that girls will perform the task faster than boys. Here’s what you should have done to compute mode: 1. 2. 3. John’s data Female Mode: 55 is only score that appears more than once so it is the mode for the females times. Male mode: The male times have no repeat values, so there is no mode. 42, 55 and 66 (each of these numbers appears twice) So what? 4.What do the modes in these sets of data tell us about female and male performance on this test? Nothing meaningful in terms of hypothesis. 5.Would the mode be more helpful to John if the score repeated nearly every trial? • No. Having a repeated score is not relevant to his hypothesis. 6.What kind of data sets would you want the mode to be a very frequently occurring number? • When you are looking for consistency! Here’s what you should have done to compute the mean... 1. Compute the mean for the females. 59.4 1. Compute the mean for the males. 63.4 1. Compute the mean for the males and females combined. (594+634)/20=61.4 4. What conclusions can be drawn about female vs. male time on the sorting task based on the means we just computed? There is a difference between average time of girls and boys; girls sort 4 seconds faster on average. 5. Can John conclude that his hypothesis was correct based on the values of the means? NO. Mean alone is not a statistically valid measure. It must be looked at in conjunction with other Here’s what you should have done to compute median... Median: First you must rearrange the data for each column in ascending order. Because there is an even amount of data (10 values per gender), you must find the median by adding the values at positions 5 and 6 and dividing by 2. Females: (55+56)/2 = 55.5 Males: (63+65)/2 = 64 3. What conclusions can you draw about these data sets by knowing the medians? • Not many. You only know that half of the girls times were faster and half slower than 55.5 seconds while half of the boys times were faster and half slower than 64 seconds. We need to know the shape of the data in order for median to have any value to us. 4. Do the medians allow you to know which group of the 2 had the fastest or slowest times? • NO. 5. Do the medians allow you to determine if your hypothesis that girls will perform the task faster than boys is correct? • NO. Skews...Tell the shape of the curve Positive (AKA skewed right): The whale is swimming to California; it is happy (positive)!! 1. On which side is the majority of the data in graph A? Left side. 1. On which side of the graph are their outliers? Right side 3. If the graph A represented the scores on a unit test, and the teacher relied on the “mean” of the test scores to determine how well her students did, would the teacher be happy or sad to have positive skew? Happy because it makes her test scores look better than they actually were! Negative (AKA skewed left): The whale is swimming to New York. It is angry (negative!!) 1.On which side is the majority of the data in graph B? Right side 1.On which side of the graph are their outliers? Left side. 1.If graph B represented the scores on a unit test, and the teacher relied on the “mean” of the test scores to determine how well her students did, would the teacher be happy or sad to have negative skew? WHY? Sad because it makes her test scores look worse than they actually were! Why “mean” can be deceptive... Mr. Smith and Mrs. Anderson gave the same final exam for their AP Economics class. Both teachers have 100 students in their classes. Both teachers reported an average score (mean) for their classes of 75 out of 100 on the final exam. From this set of data, which of the following can we conclude? A. Mr. Smith’s and Mrs. Anderson’s students performed equally well on the final exam. B. The majority of the students in both classes scored a C on the final exam (assuming they grade on a standard grade scale.) C. None of the above!! Why none of the above? In order to compare the 2 classes we need to know the range of scores. We would also want to know if the distribution (and therefore the mean) was skewed due to an extreme high or extreme low score. Descriptive Stats Part 3 Measurements of variability: Range Which of the teacher’s has the biggest range? •Mrs. Anderson! Her range is 100! (+/- 10) •Mr. Smith’s range is only 39, meaning the scores in his data set all fall within 39 points of each other (+/- 10) SO WHAT? Which of the following can we conclude based on knowing just the range? A. Mr. Smith did a better job of preparing his students for the test B. Mr. Smith has students that are better test takers C. Mr. Smith’s students studied more effectively for the test D. On that particular day, Mr. Smith’s students were able to score better. E. In essence, we can’t conclude much!! The data don’t tell us WHY the classes received the scores they did; it just paints a picture of how the class scores compare. Descriptive Stats Part 3 continued Measurements of variability: Standard deviation and z scores... The mean on Mrs. Hunter’s chemistry test is 75. The standard deviation for her data is 15. Her data is skewed right. 1.Let’s first draw a rough graph of her data. 1.What does the “15” tell us about the scores in her set of data? They are spread out quite far from the mean—the average distance of all scores less than and greater than 75 is 15 3.What does the right skew tell us about outliers and the mean? •A few high scores are making her mean artificially high 4.Horace has a z score of +1.0. What was his actual test score? •the z score tells us Horace’s test score falls to the right of the mean 1 unit of standard deviation. Standard dev. (15) + mean (75)= real score. His score was 90. 5.Jillian has a z score of -1.5. What was her actual test score? •The z score tells us Jillian’s test score falls 1.5 units of standard deviation to the left of the mean. •1.5x15 = 22.5 •Mean of 75 – 22.5 = 52.5 Meet your new best friends: The Normal Curve and the Empirical Rule If you add percentages, you will see that approximately: • ________ % of the distribution lies within one standard deviation of the mean. • _______ % of the distribution lies within two standard deviations of the mean. • ________ % of the distribution lies within three standard deviations of the mean. These percentages are known as the "empirical rule" What you need to know and be able to do... • • For purposes of this class and the AP exam, you do not have to understand when or why a normal curve is used You DO NEED TO KNOW – the empirical rule values – how much data falls within 1, 2, and 3 standard deviations of a normal curve – the percentiles associated with each z score John uses the means of both the male and female groups to conclude that girls are faster than boys at the sorting task so his hypothesis was correct. His teacher tells him to analyze whether his experiment was designed to eliminate sampling error. 1. Did he use proper sampling techniques to generate his test participants (sample)? A. first identify the population to which this hypothesis applies a) the characteristics required for a sample may be dependent upon the independent variable (if the ind. var is a human characteristics such as height, weight, gender, race, age) OR b) the goal of the sample may be to make it diverse and representative of the general population c) to ensure representative sampling, an experimenter may use stratified sampling to make sure that the sample proportionally represents the general population for a given characteristic 2. Once the sample population was identified, did he use random assignment to produce his female and male participant lists? A. Out of 1,000 students at his school, did he randomly choose 10 male and 10 female students? 3. Was the study blind or double-blind in order to eliminate participant or experimenter bias? Solutions to “Andrea’s” results 1. Andrea just got her ACT results (which are distributed normally) and they say she scored in the 99.87 percentile for reading. a) What does that tell her about her score compared to the rest of the ACT test takers? b) Approx how many a. She got a higher standard score than 99.87% of deviations is she those who took the from the mean? same test. b. Her score is 3 standard deviations from the mean (z score = +3.0) ANSWERS: Reviewing the rules of the normal curve 2. What percent of data always falls within 1 standard deviation of the mean on a normal curve? 68% You have to account for 1 standard deviation in both directions. ANSWERS: Reviewing the rules of the normal curve 2. What percent of data always falls within 2 standard deviations of the mean on a normal curve? 95% You have to account for 2 standard deviation in both directions. ANSWERS: Reviewing the rules of the normal curve 3. What kind of skew does a normal curve have? NO skew. It is not being pulled left or right because it is SYMMETRICAL Because the mean = the median, we know it is not skewed. 5. Dana just got back is CSAP scores which were normally distributed. His z score for math was -3.0. His raw score was 316. His brother had a z score of +3.0 and a raw score of 516. a) b) Solutions Dana’s CSAP scores What was the mean for the CSAP math test? What was the standard deviation? a. Because mean will be symmetrically located between z scores or -3 and + 3, mean must be half way between 316 and 516. Mean = (316+516)/2 = 416 b. Measure the difference (distance) between one of the scores and the mean. •516-416=100 • The difference, 100, represents 3 standard deviations from the mean •100/3 = 33.3 Standard deviation is 33.3 Computing standard of deviation in 6 simple steps!! Step 1: Calculate the mean for the data set Step 2: find the distance of each score from the mean Step 3: Square each deviation Step 4: Sum the squared deviations Step 5: Divide your sum by total # of scores Step 6: Square root of the answer from step 5 SUM= 2324 2324/10 = 232.4 sq root of 232.4 = standard of deviation of 15.2