* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Chapter 2.3 the use of statistics in psychology
Survey
Document related concepts
Transcript
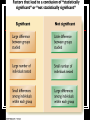
the use of statistics in psychology statistics Essential Occasionally misleading Two types – mathematical summaries of results Descriptive – statements about large populations derived from small samples Inferential Descriptive statistics Measures of the central score Mean – the average score, found by adding all the scores together and then dividing by the number of scores Vulnerable to skewing by very high scores Measures of the central score ii Median – the middle score after the scores are arranged from highest to lowest Much less sensitive to skewing Central score measures iii Mode – the most common score Usually of limited interest Measures of variation Enough about the “central score”, how the scores differ, or vary, within a distribution is just as important The Range – the difference between the highest and lowest score The Standard Deviation – a measurement of the amount of variation among scores in a normal distribution examples Sample distribution – 1,2,3,3,21 Measures of Central Score Mean = 6 Median = 3 Variation Range = 20 Standard Deviation = 7.5 Mode = 3 Inferential statistics We found a difference between the experimental group and the control group. What does that tell us about the population we are interested in? Could the difference have resulted from chance? Inferential statistics ii Procedures used to decide whether differences really exist between sets of numbers Does our experimental group significantly differ from the population from which it was drawn? significance tests Assess the odds that we could have gotten such a difference (between the experimental and the control group) at random We want to prove that the difference would only occur 5% of the time by luck If we can, then the difference is significant – our experiment worked. Data set 1 Experimental group 3 10 10 10 2 35 Mean=7; SD=4.1 Control group 5 7 6 5 7 30 Mean= 6; SD= 1 Inferential statistics Statements about large populations taken from small samples How can we be sure that our results really mean something? That they apply to the entire population and not just to the sample? data set 2 Experimental group 10 6 7 9 8 7 10 8 Mean = 8 6 SD = 1.5 9 80 Control group 7 6 5 10 2 4 8 6 Mean = 6 5 SD = 2.2 7 60 In other words… If the experimental group’s free throw shooting performance had not been affected by the relaxation technique, we would only see such a difference between the two groups in 1 out of 500 occasions. We can reasonably claim that the results supported our hypothesis.