Download Document

統計推論
(An Overview Of Statistical Inference)
The statistical inference
contains two parts
• Estimation（參數估計；母數估計）
 點估計
 區間估計
• Hypothesis Testing（假說檢定；
假設考驗）
 有母數分析（利用常態分布的特性）
 無母數分析
CHAPTER 6
Estimation
(參數估計)
Definition ＿統計推論
• Statistical inference is the
procedure by which we
reach a conclusion about a
population on the basis of
the information contained
in a sample drawn from
that population.
Definition＿點估計
• A point estimate is a single
numerical value used to
estimate the corresponding
population parameter.
Definition ＿區間估計
• An interval estimate consists
of two numerical values
defining a range of values
that, with a specified degree
of confidence, we feel
includes the parameter being
estimated.
母群平均值的估計
• Estimators are usually
presented as formulas. For
example,
x

x
n
i
Definition＿不偏估計
• An estimator, say, T, of the
parameter θ is said to be
an unbiased estimator of θ
if E (T )＝θ.
Definition ＿樣本
• The sampled population
is the population from
which one actually draws
a sample.
Definition＿標的母群
• The target population is
the population about
which one wishes to make
an inference.
Point Estimation （點估計）
• sample statistics
population parameters
X＝ΣXI∕n
S2＝Σ(XI－X)2∕(n－1)
＝[ΣXi2－(ΣX)2∕n]∕(n－1)
μ ＝ΣXI∕N
σ2 ＝Σ(XI －μ)2∕N
＝[ΣXi2 －Nμ2 ]∕N
• Principles of estimation
–
unbiasedness（不偏性）: 期望值等於真值才是不偏估計
E(X)＝μ
–
–
–
E(S2)＝σ2
consistency（一致性） : 樣本數愈大愈趨近真值
efficiency （有效性）: 估計數的變異最小
sufficiency（充分性） : 充分的樣本所估計出的
Interval Estimation
（區間估計）
Confidence Interval of population mean
﹦Point Estimator ± (reliability
coefficient) × (standard error of
point Estimator)
(6.2.1)
x  z(1α
σx
2)
(6.2.2)
§μ的區間估計（95％信賴區間）
• 當樣本平均值(X)能座落在μ ±1.96(σ/
圍內時，則μ就能座落在X ±1.96(σ/
n) 範
)範
n
圍內(此︰Z.975=1.96)
• 估計參數有95％的機率可能座落之範圍
• 點估計 ±（ 標準化值* 點估計的標準誤）
• X ±Z.975 SEM = X ±1.96(σ/
n)
Example 6.2.1
• Suppose a researcher, interested in
obtaining an estimate of the average level
of some enzyme in a certain human
population, takes a sample of 10
individuals, determines the level of the
enzyme in each, and computes a sample
mean of x ＝22. Suppose further it is
known that the variable of interest is
approximately normally distributed with a
variance of 45. We wish to estimate μ.
• μ的95% C.I.等於： x  2σ x
45
22  2
10
22  2( 2.1213)
17.76, 26.24
Example 6.2.2
• A physical therapist wished to estimate,
with 99 percent confidence, the mean
maximal strength of a particular muscle in
a certain group of individuals. He is willing
to assume that strength scores are
approximately normally distributed with a
variance of 144. A sample of 15 subjects
who participated in the experiment yielded
a mean of 84.3.
z  2.58
Z.995=2.58
σ x  12 / 15  3.0984
84.3  2.58(3.0984)
84.3  8.0
76.3, 92.3
Example 6.2.3
• Punctuality of patients in keeping
appointments is of interest to a research
team. In a study of patient flow through the
offices of general practitioners, it was found
that a sample of 35 patients were 17.2,
minutes late for appointments, on the
average. Previous research had shown the
standard deviation to be about 8 minutes.
The population distribution was felt to be
nonnormal. What is the 90 percent
confidence interval for μ, the true mean
amount of time late for appointments?
σ x  8/ 35  1.3522
90% C.I.  17.2  1.645(1.3522)  17.2  2.2  15.0, 19.4
Confidence interval for the difference
between two population means
• When the population variances
are known, the 100(1－α)
percent confidence interval for
μ1－μ2 is given by
( x 1  x 2 )  z1α 2
σ
σ

n1 n2
2
1
2
2
§(μ1-μ2)的區間估計（95％信賴區間）
• 估計參數有95％的機率可能座落之範圍
• 點估計 ±（ 標準化值* 點估計的標準誤）
•
(X 1- X 2 ) ±Z.975 SE
•=(X 1- X 2 )
±1.96σ
(X 1- X 2 )
(X 1- X 2 )
•= (X 1- X 2 ) ±1.96 σ12/n1+ σ22/n2
Example 6.4.1
• A research team is interested in the difference
between serum uric acid levels in patients with
and without Down’s syndrome. In a large hospital
for the treatment of the mentally retarded, a
sample of 12 individuals with Down’s syndrome
yielded a mean of x1＝4.5 mg/100 ml. In a general
hospital a sample of 15 normal individuals of the
same age and sex were found to have a mean
value of x2＝3.4. If it is reasonable to assume that
the two populations of values are normally
distributed with variances equal to 1 and 1.5, find
the 95 percent confidence interval for μ1－μ2.
x 1  x 2  4.5  3.4  1.1
σ x1  x 2 
σ12 σ 22


n1
n2
1
1.5

 .4282
12 15
95% C.I.  1.1  1.96(.4282)  1.1  .84  .26, 1.94
Example 6.4.2
• Motivated by an awareness of the existence of a body of
controversial literature suggesting that stress, anxiety, and
depression are harmful to the immune system, Gorman et al.
conducted a study in which the subjects were homosexual
men, some of whom were HIV positive and some of whom
were HIV negative. Data were collected on a wide variety of
medical, immunological, psychiatric, and neurological
measures, one of which was the number of CD4+ cells in the
blood. The mean number of CD4+ cells for the 112 men with
HIV infection was 401.8 with a standard deviation of 226.4.
For the 75 men without HIV infection the mean and standard
deviation were 828.2 and 274.9, respectively. We wish to
construct a 99 percent confidence interval for the difference
between population means.
828.2  401.8  426.4  the reliability factor  2.58
274.9 2 226.4 2
the estimated standard error  s x1x 2 

 38.2786
75
112
99% C.I.  426.4  2.58(38.2786)  327.6, 525.2
Confidence Interval of
Population proportion
• Estimator ± (reliability
coefficient) × (standard error)
•
(6.5.1)
§ 二項分布π的區間估計（95％信賴區間）
• 估計參數有95％的機率可能座落之範圍
• 點估計 ±（ 標準化值* 點估計的標準誤）
• p ± Z.975 SEp= p ±1.96 σp
• p ± Z.975 SEp= p ±1.96
= p ±1.96
π（1－π）
n
p（1－p）
n
Example 6.5.1
• Mothers et al. (A-12) found that in a
sample of 591 patients admitted to a
psychiatric hospital, 204 admitted to
using cannabis at least once in their
lifetime. We wish to construct a 95
percent confidence interval for the
proportion of lifetime cannabis users
in the sampled population of
psychiatric hospital admissions.
^
p  204 591  .3452
^
^
σ ^  p(1  p) n  (.3452)(. 6548) 591  .01956
p
95% C.I.  .3452  1.96(.01956)  .3452  .0383  .3069, .3835
Confidence interval for the difference
between two population proportions
• The standard error of the estimate
usually must be estimated by
^
^
σ p1  p2 
^
^
^
^
^
p1(1  p1 )
p2 (1  p2 )

n1
n2
• 100(1－α) percent confidence
interval for 1－ 2 is given by
§兩個二項分布成功率差異 (π1 - π2)的
區間估計（95％信賴區間）
• 估計參數有95％的機率可能座落之範圍
• 點估計 ±（ 標準化值* 點估計的標準誤）
• (p1- p2 )
±Z.975 SE
(p11 -- pp22 ))
(p
•= (p1 - p2 ) ±1.96
π1 (1-π1 )/n1 +π2 (1-π2 )/n2
•= (p1 - p2 ) ±1.96
p1 (1-p1 )/n1 +p2 (1-p2 )/n2
Example 6.6.1
• Borst et al. investigated the relation of ego development, age,
gender, and diagnosis to suicidality among adolescent
psychiatric inpatients. Their sample consisted of 96 boys and
123 girls between the ages of 12 and 16 years selected from
admissions to a child and adolescent unit of a private psychiatric
hospital. Suicide attempts were reported by 18 of the boys and
60 of the girls. Let us assume that the girls behave like a simple
random sample from a population of similar girls and that the
boys likewise may be considered a simple random sample from
a population of similar boys. For these two populations, we wish
to construct a 99 percent confidence interval for the difference
between the proportions of suicide attempters.
^
p G  60 123  .4878
^
^
p B  18 96  .1875
^
p G  p B  .4878  .1875  .3003
(.4878)(. 5122) (.1875)(. 8125)

 .0602
123
96
99% C.I.  .3003  2.58(.0602)  .1450, .4556
s pG  pB 
§布瓦松分布成功數μ的區間估計
（95％信賴區間）
• 估計參數有95％的機率可能座落之範圍
• 點估計 ±（ 標準化值* 點估計的標準誤）
• x ±Z.975 SEx= x ±1.96
x
§兩個布瓦松分布成功數差異 (μ1-μ2)的區
間估計（95％信賴區間）
• 估計參數有95％的機率可能座落之範圍
• 點估計 ±（ 標準化值* 點估計的標準誤）
• (x -x )
1 2
±Z.975 SE
•= (x -x )
1 2
±1.96
(X 1- X 2 )

x1 + x2
Interval Estimation
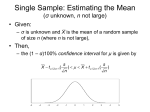
• μ的95% Confident Interval（信賴區間）：
x  z(1α 2 )σ x
• t-Distribution:
– In repeated sampling, the frequency distribution curve of
sample means from normal population should be normal,
but, when σ2 is estimated by S2 and the sampling size is
small ( < 30), the frequency distribution curve of (X－
μ)∕SX should be leptokurtic and is called: " student's tdistribution ".
– Degree of Freedom（自由度；df）
• μ的95% C.I.等於：
X ±Z(1－α∕2) σ/ n
X ±t(1－α∕2；df) S / n
§z分布與 t 分布
• X~N(μ, σ2)
x

t(df)=(x- µ)/s
Z =(x- µ)/ σσ
t(df)~t(0,1)
Z~N(0,1)
95％
Z
-1.96
+1.96
<95％
t.025-1.96
+1.96
t(df)
t.975
Properties of the t Distribution
• It has a mean of 0.
• It is symmetrical about the mean.
• In general, it has a variance greater than
1, but the variance approaches 1 as the
sample size becomes large. For df>2 , the
variance of the t distribution is df/(df-2),
where df is the degrees of freedom.
Alternatively, since here df=n-1 for n>3,
we may write the variance of the t
distribution as (n-1)/(n-3)
• The variable t ranges from –∞ to + ∞.
Properties of the t Distribution
• The t distribution is really a family of
distributions, since there is a different
distribution for each sample value of
n -1, the divisor used in computing s 2.
We recall that n -1 is referred to as
degrees of freedom.
Properties of the t Distribution
• Compared to the normal distribution
the t distribution is less peaked in the
center and has higher tails. The t
distribution approaches the normal
distribution as n-1 approaches infinity.
Confidence Intervals Using t
• estimator ± (reliability coefficient) ×
(standard error)
• When sampling is from a normal
distribution whose standard
deviation, σ is unknown, the 100 (1
－α) percent confidence interval for
the population mean, μ, is given by
x  t (1α / 2)
s
n
Example 6.3.1
• It is a study to evaluate the effect of on-the-job body mechanics
instruction on the work performance of newly employed young
workers. The experimental group received one hour of back
school training provided by an occupational therapist. The
control group did not receive this training. A criterion-referenced
Body Mechanics Evaluation Checklist was used to evaluate each
worker’s lifting, lowering, pulling, and transferring of objects in
the work environment. A correctly performed task received a
score of 1. The 15 control subjects, which behave as a random
sample from a population, made a mean score of 11.53 on the
evaluation with a standard deviation of 3.681. We wish to use
these sample data to estimate the mean score for the population.
x  11.53
standard error  s n  3.681 15  .9504
degree freedom  n  1  15  1  14
t.975  2.1448
95% C.I.  11.53  2.1448(.9504)  11.53  2.04  9.49, 13.57
假設兩母群的變異數相等
The pooled variance of the estimate ( X 1- X 2 )
Ｓ
The standard error of the estimate ( X 1- X 2 )
The 100(1-α) percent confidence interval for (μ1-μ2)
Example 6.4.3
• The purpose of a study by Stone et al. was to determine the effects of
long-term exercise intervention on corporate executives enrolled in a
supervised fitness program. Data were collected on 13 subjects (the
exercise group) who voluntarily entered a supervised exercise program
and remained active for an average of 13 years and 17 subjects (the
sedentary group) who elected not to join the fitness program. Among
the data collected on the subjects was maximum number of sit-ups
completed in 30 seconds. The exercise group had a mean and standard
deviation for this variable of 21.0 and 4.9, respectively. The mean and
standard deviation for the sedentary group were 12.1 and 5.6,
respectively. We assume that the two populations of overall muscle
condition measures are approximately normally distributed and that the
two population variances are equal. We wish to construct a 95 percent
confidence interval for the difference between the means of the
populations represented by these two samples.
2
2
(
13

1
)(
4
.
9
)

(
17

1
)(
5
.
6
)
s p2 
 28.21
13  17  2
the reliability factor  2.0484 =t.975(28)
95% C.I.  (21.0 - 12.1)  2.0484
28.21 28.21

 8.9  4.0085  4.9, 12.9
13
17
假設兩母群的變異數不相等
若兩母群的變異數不相等時，則 t 分布的
形狀不能遵循自由度為(n1+n2-2)的分布，
必須做調整。調整的方法有兩種︰（1）調
整t 的判定值，（2）調整t 的自由度；兩
種方法的權重均為該樣本平均數的變異數。
（1）調整t 的判定值
Example 6.4.4
• In the study by Stone et al. described in Example
6.4.3, the investigators also reported the following
information on a measure of overall muscle
condition scores made by the subjects:
degrees of freeom  12 1  .05 2  .975 t1  2.1788
degrees of freeom  16 1  .05 2  .975 t 2  2.1199
(.3 2 13)( 2.1788)  (1.0 2 17)( 2.1199) .139784
t' 

2
2
.065747
(.3 13)  (1.0 17)
.3 2 1.0 2
95% C.I.  (4.5  3.7)  2.1261

 .8  2.1261(.25641101)  .25, 1.34
13 17
假設兩母群的變異數不相等
（2）調整t分布的自由度
1/dfc=(c12/df1)+ (c22/df2)
c1 = Sx12/(Sx12 + Sx22 ) = (S12/n1) / [(S12/n1) + (S22/n2 )]
c2 = (1-c1) = Sx22/(Sx12 + Sx22 ) = (S22/n2) / [(S12/n1) + (S22/n2 ) ]
{(S12/n1)/[(S12/n1)+(S22/n2)]}2
{(S12/n1)/[(S12/n1)+(S22/n2)]}2
+
dfc=
df
df
1
dfc=
df1*( n2 S12 )2+ df2*(n1 S22 )2
[(n2 S12)+(n1 S22)]2
2
Example 6.4.4
• In the study by Stone et al. described in Example
6.4.3, the investigators also reported the following
information on a measure of overall muscle
condition scores made by the subjects:
df1=12
S1=0.3
SE12=S12/n1=0.0069
df2=16
S2=1.0
SE22=S22/n2=0.0588
c1= SE12/(SE12+ SE22) =0.0069/0.0657=0.105
95%C.I.(μ1－μ2)=
c2= 1- c1= 1-0.105 =0.895
1/dfc=(c12/df1)+ (c22/df2)
t.975(16.925)
=0.1052/12 )+ (0.8952/16) =0.0510
=(4.5-3.7)±2.093*0.2564
dfc=16.925
t.975(16.925) =2.093
SQRT(SE12+ SE22)=0.06571/2 =0.2564
=0.8±0.5367=0.2633~1.3367
Determination of sample size--For estimation of population mean
If d＝unit on either side of the estimator,
then:
d＝(reliability coefficient) ×(standard error)
σ
dz
n
σ
d z
n
N n
N 1
z 2σ 2
n 2
d
Nz2σ 2
n 2
d (N  1)  z 2σ 2
Example 6.7.1
• A health department nutritionist, wishing to
conduct a survey among a population of teenage
girls to determine their average daily protein
intake (measured in grams), is seeking the advice
of a biostatistician relative to the sample size that
should be taken. What procedure does the
biostatistician follow in providing assistance to the
nutritionist? Before the statistician can be of help
to the nutritionist, the latter must provide three
items of information: the desired width of the
confidence interval(5 grams), the level of
confidence desired(95%C.I.), and the magnitude
of the population variance (=20 grams).
2
2
(1.96) (20)
n
 61.47
2
(5)
Determination of sample size---
For estimation of population proportion
d＝(reliability coefficient) ×(standard error)
• d= Z * (p q / n) ½
2
z
pq
• n
d2
q  1 p
Nz 2 pq
• n 2
2
d (N  1)  z pq
Example 6.8.1
• A survey is being planned to
determine what proportion of families
in a certain area are medically
indigent. It is believed that the
proportion cannot be greater than .35.
A 95 percent confidence interval is
desired with d＝.05. What size sample
of families should be selected?
2
(1.96) (.35)(.65)
n

349
.
6
2
(.05)
• Sampling with Replacement
2
s
i
0  2      2  0 200
E (s )  n 

8
25
25
N
E(s 2 )  σ 2 s 2   ( xi  x)2 (n  1) σ 2   ( xi  μ )2 N
2
• Sampling Without Replacement
E (s ) 
2
2
s
 i
N
S2 
Cn
2  8      2 100


 10
10
10
2
(
x

μ
)
(N  1)
 i
• E(s 2)＝σ2, when sampling is with
replacement
• E(s 2)＝s 2, when sampling is without
replacement
Inference of population
Variance
n
• S 2＝ (X-X) 2/(n-1)＝ 2
• S 2 ＝[ (X-X) 2 / 2 ] / [(n-1)/ 2 ]
• S 2 ＝[ Z 2 ] / [(n-1) /  2 ]
• S 2 ＝(n-1) 2 / [(n-1) /  2 ]
•  2 ＝S 2 (n-1) / (n-1) 2
•  2 ＝SS / (n-1) 2
Confidence Interval of
Population Variance（ 2）
•
•
•
X
X
1
(n  1)s
2
 2

 X 1(α 2)
2
2
2
(n  1)s σ (n  1)s
σ
2
α2
2
X
2
α2
(n  1)s
(n  1)s
2
σ  2
2
Xα 2
X 1(α 2)
2
(n  1)s 2
σ 
2
X 1(α 2)
2
2
1(α 2)
(n  1)s
(n  1)s
2
σ 
2
2
X 1(α 2)
Xα 2
2
(n  1)s 2
2
Xα 2
2
Example 6.9.1
• In a study of the effect of diet on low-density
lipoprotein cholesterol, Rassias et al. (A-21) used
as subjects 12 mildly hypercholesterolemic men
and women. The plasma cholesterol levels (mmol/L)
of the subjects were as follows: 6.0, 6.4, 7.0, 5.8,
6.0, 5.8, 5.9, 6.7, 6.1, 6.5, 6.3, 5.8. Let us assume
that these 12 subjects behave as a simple random
sample of subjects from a normally distributed
population of similar subjects. We wish to estimate,
from the data of this sample, the variance of the
plasma cholesterol levels in the population with a
95 percent confidence interval.
s 2  .391868 df  n  1  11 X 12(α 2)  21.920
Xα2 2  3.1816
11(.391868)
11(.391868)
 σ2 
 .196649087  σ 2  1.35483656
21.920
3.1816
95% C.I. for σ  .4434  σ  1.1640
95% C.I. for σ 2 
Confidence Interval for [σ12/σ22]
• F=S12/S22
• ={(n1-1)2/[(n1-1)/2]}/{(n2-1)2/[(n2-1)/2]}
• ={(n1-1)2/(n1-1)}/{(n2-1)2/(n2-1)}
Fα 2
s12 σ12
 2 2  F1(α 2)
s2 σ 2
•
Fα 2
s12 σ 22
 2  2  F1(α 2)
s2 σ1
σ 22 F1(α 2)
 2 2 2
2
2
s1 s2 σ1 s1 s2
•
s12 s 22 σ12 s12 s 22
 2 
Fα 2
σ 2 F1(α 2)
s12 s 22 σ12 s12 s 22
 2 
F1(α 2) σ 2
Fα 2
•
Fα 2
Confidence Interval for [σ12/σ22]
s s
σ
s s


•
F1(α 2) σ
Fα 2
2
1
2
2
2
1
2
2
2
1
2
1
2
2
s
LCL 
s
•
2
1
2
2
s
UCL 
s
2
2
F1α ,df1,df2 
1
Fα ,df1,df2
1
Fα
2,df2 ,df1
1
1 F1(α
2 ),df1,df 2
Example 6.10.1
• Goldberg et al. conducted a study to determine if an
acute dose of dextroamphetamine might have positive
effects on affect and cognition in schizophrenic patients
amintained on a regimen of haloperidol. Among the
variables measured was the change in patients’
tension-anxiety states. For n2＝4 patients who
responded to amphetamine, the standard deviation for
this measurement was 3.4. For n1＝11 patients who did
not respond, the standard deviation was 5.8. Let us
assume that these patients constitute independent
simple random samples from populations of a normally
distributed variable in both populations. We wish to
construct a 95 percent confidence interval for the ratio
of the variances of these two populations.
n1  11 n2  4 s12  (5.8) 2  33.64 s 22  (3.4)2  11.56
df1  10 df2  3 α  .05 F.025  .20704 F.975  14.42
33.64 11.56 σ12
33.64 11.56
 2 
14.42
.20704
σ2
σ12
.2018  2  14.0554
σ2
To be continued…..
Thanks for your attention