Download Descriptive Statistics

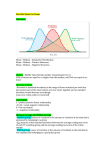
Session III
Introduction to Basic Data Analysis
Dr. L. Jeyaseelan
Professor
Department of Biostatistics
Christian Medical College, Vellore.
About Statistics Class:
Some one said
“ If I had only one day to live,
I would live it in my statistics class -
About Statistics Class (Contd..):
“it would seem so much longer”
What is Statistics?
A science of:
• Collecting numerical information (data)
• Evaluating the numerical information
(classify, summarize, organize,
analyze)
•Drawing conclusions based on evaluation
Statistical Applications
• Descriptive Statistics
Summarizes or describes the data set at hand.
Evaluate the data set for patterns and reduce
information to a convenient form.
• Inferential Statistics
Use sample data to make estimates or
predictions about a larger set of data.
Types of Data
Qualitative Data
Quantitative Data
Nominal
Discrete
Ordinal
Continuous
Interval
Ratio
Terms Describing Data
Quantitative Data:
There is a natural numeric scale
(can be subdivided into interval and ratio data)
Example:- age, height, weight
Qualitative Data:
Measuring a characteristic for which there is no
natural numeric scale
(can be subdivided into nominal and ordinal data)
Example:- Gender, Eye color
Quantitative data
Discrete Data :
• Values are distinct and separate.
• Values are invariably whole numbers.
Example: Number of children in a family.
Continuous Data :
• Those which have uninterrupted range of values.
• Can assume either integral or fractional values.
Example : Height, Weight, Age
Scales of Measurement (Qualitative data)
Nominal data :
To classify characteristics of people, objects or events into
categories.
Example: Gender (Male / Female).
Ordinal data (Ranking scale) :
Characteristics can be put into ordered categories.
Example: Socio-economic status (Low/ Medium/ High).
DESCRIPTIVE STATISTICS
Descriptive
Statistics
Measures of central tendency are statistics that
summarize a distribution of scores by reporting the most
typical or representative value of the distribution.
Measures of dispersion are statistics that indicate the
amount of variety or heterogeneity in a distribution of
scores.
Descriptive Statistics
• Measures of Central Tendency
– Mean
– Median
– Mode
• Measures of Dispersion
– Range
– Variance
– Standard Deviation
Mean:
• Single value that could describes the characteristics of
the entire data
• Most representative
• Arithmetic mean or average
Mean birth weight, mean DBP
Merits:
Easy to Understand and compute
Based on the value of every item in the series
Limitations:
Affected by extreme values
Not useful for the study of qualities like
intelligence, honesty and character
Computing Mean - Sample Problem
Consider the number of children in 6 families. In the
first family there are 4 children, in the second there are
2, in the third 5, in fourth & fifth 3, and in the sixth, 4.
Find average number of children per family.
Step 1: Summing the scores
ie., 4+2+5+3+3+4 = 21
Step 2: Dividing by the number of families
ie., 21 ÷ 6 = 3.5
Interpretation:
The average number of children per family is 3.5
Median:
• Arrange the data in ascending or descending order.
Middle value is median.
•Not influenced by extreme values
• Unique and easy to calculate
• More appropriate when the measure is Duration
(survival), age etc
Computing the Median
• To compute the median, we sort the values from low
to high. The median is the middle score.
• If the number of cases in the sample is an odd
number, the middle case is the case above and below
which the same number of cases occur.
( e.g. 1 2 3 4 5 )
• If the number of cases in the sample is an even
number, there will be two middle scores and the
median is halfway between these two middle scores.
(e.g. 1 2 3 4 5 6 )
Mode:
• Most commonly occurring observation.
• Not Unique.
• Not very frequently used.
• Used in investigation of an epidemic.
Computing the Mode
The mode can be read directly from the
frequency distribution table. The mode for
Race is the category 5 = White which has
the largest frequency (231).
Is that Enough?
Mean, Median and Mode
Example:
Two sleep producing drugs were administered for
two group of patients.
Drug A: 6,2,4,3,5,2
hours
mean= 3.7
Drug B: 1,6,7,1,2,6
hours
mean= 3.7
How do we measure the variability?
1. Measure the deviance from mean for each
observation.
Example:
4, 5, 3
Mean = 12/3 = 4
xi - Mean
x1
4
- 4
= 0
x2
5
- 4
= 1
x3
3
- 4
= -1
2. Square the deviance to get rid of the sign problem and
find the total (sum).
Example:
4, 5, 3
Mean = 12/3 = 4
(xi - Mean)2
xi - Mean
x1
4
- 4
= 0
0
x2
5
- 4
= 1
1
x3
3
- 4
= -1
1
0
2
Total
3. Find the average of all deviance:
 (xi - Mean)2
Variance = -----------------n
=
2
------------------- = .66
3
Standard Deviation =  var =  .66 = .81
Variance or Standard Deviation:
On an average, how far each and every
observation deviates from the mean.
About the study itself.
Standard Error:
• Sample mean is an estimate of the population
mean.
• Mean birth weight of 100 babies is 2700g
(sd=200).
• Can we say that the population mean is also
2700g?
• Uncertainty associated with our estimate 2700g
• How do we measure the uncertainty?
Standard Error (contd..):
Take many samples of same size from the population.
• Assess the variability of such means.
• These means follow Normal
distribution.
• Mean of these means is the population
mean.
• This variability can be estimated from a single
study.
• SE = /n
Distributions of 16 samples of size 50 from the
Normal distribution.
Normal Distribution
• Bell shaped
• Symmetrical about its mean
• Mean, Median and Mode are same
• Total area is one square unit
Point Estimate
The prevalence of HIV in Tamil Nadu was
1.8% in 1998 and .7% in 2003.
As a special honey moon offer we will provide you a double
Bed room at the cost of a single room.
Confidence Interval:
• Means of different samples follows normal
distribution.
• Mean ± 1.96 SD covers 95% of the area.
• These limits which will cover population mean.
• 5% of the time these limits may not cover the
population mean.
Scatter Plot of 95% CI:
Confidence intervals for mean serum albumin constructed
from 100 random samples of size 25. The vertical lines
show the range within which 95% of sample means are
expected to fall.
The Distribution of Data
(Rule of thumb)
The statistical & clinical applications of the term “normal” are
often confused and vague
SD>1/2 mean
Skewed/Non-normal data
Note: Applicable only for variable where negative values are
impossible
Altman BMJ1991.
Comparison of TLV by Ultrasound and
BSA (Western Population)
30
20
10
Std. Dev = 213.15
Mean = 40.9
N = 238.00
0
60
50
40
30
20
10
0.
0.
0.
0.
0.
0
0
0
0
0
0
.0
.0
.0
.0
.0
0.
00
00
00
00
00
0
0 . .0
00
-1
-2
-3
-4
-5
-6
Difference between the W estern formula using BSA and TLV
Contd..
•
Data described with a SD that exceeds onehalf the mean are non-normally distributed
(assuming that negative values are
impossible) and should be described with the
median and range/interquartile range
•
Subtracting the median from the mean
produces a crude estimate of the skewness of
the data:
The larger the difference, the greater the
skewness
Presentation of Summary Statistics :
SD or SE
•
The terms “standard error” and “Standard deviation” are
often confused.
•
The contrast between these two terms reflects the
important distinction between data description and
precision/inference.
•
SD: Is a measure of variability and explains how widely
scattered some measurements are in a group.
•
SE: Applicable for large samples & indicates the
uncertainly around the estimate of the mean
measurement.
Standard Deviation
Description of data:
Example:
If the mean weight of a sample of 100 men is 72kg
and the SD is 8kg.
Assuming normal distribution 68% of the men are
expected to weigh between
64 and 80kg.
Standard Error
72kg is also the best estimate of the mean
weight of all men in the population.
How precise is the estimate 72kg?.
While testing hypothesis,
Difference in mean or proportions
between groups.
Table1: Baseline characteristics of 2188 children with non-severe
pneumonia randomised to 3 days or 5 days of treatment with amoxicillin.
Values are numbers (percentages) of patients unless stated otherwise
Characteristic
3 day treatment
(n=1095)
5 day treatment
(n=1093)
Mean (SD) Age (months)
17.0 (13.3)
16.9 (13.0)
Mean (SD) height (cm)
74.8 (10.98)
74.8 (10.75)
Mean (SD) weight (kg)
8.7 (2.49)
8.7 (2.4)
Mean (SD)duration of illness days)
4.7 (3.43)
4.5 (3.12)
Mean (SD) temperature (oC)
37.1 (0.66)
37.2 (0.67)
Mean (SD) respiratory rate
(breath / minute):
2 – 11 months old
12 – 59 months old
56.4 (5.02)
47.3 (5.58)
56.0 (4.54)
47.9 (6.1)
Male
685 (62.6)
676 (61.8)
Age (months):
2 – 11
12 – 59
479 (43.7)
616 (56.3)
475 (43.5)
618 (56.5)
Weight for height z score*:
-2 to -1
-3 - 2
300 (27.4)
188 (17.2)
303 (27.7)
183 (16.7)
Table1 (Cont….)
Characteristic
3 day treatment
(n=1095)
5 day treatment
(n=1093)
Duration of illness (days):
3
3
538 (49.1)
557 (50.9)
540 (49.4)
553 (50.6)
Fever
833 (76.1)
850 (77.8)
Cough
1081 (98.7)
1078 (98.6)
Difficulty in breathing
417 (38.1)
387 (35.4)
Vomiting
135 (12.3)
141 (12.9)
Diahorrea
71 (6.5)
55 (5.0)
Excess respiratory rate (breaths / minute)
 10
 10
903 (82.5)
192 (17.5)
881 (80.6)
212 (19.4)
Wheeze present
140 (12.8)
147 (13.4)
1031 (94.2)
937 (85.6)
1026 (93.9)
928 (84.9)
252 (23.0)
261 (23.9)
Adherence to treatment:
At day 3
At day 5
RSV Positive
*Z score given as number of standard deviations from normal value.
†Rate above the age specific cut off
RSV=respiratory syncytial virus.
ISCAP Study Group BMJ 2004;328;791
THANKS