* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Chapter 6 PowerPoint
Survey
Document related concepts
Transcript
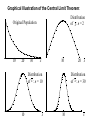
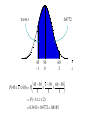
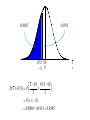
Chapter 6 Sampling Distributions Those who jump off a bridge in Paris are in Seine. A backward poet writes inverse. A man's home is his castle, in a manor of speaking. Sampling The Need Advantages Get information about a population without checking the entire population Cost Time Accuracy (can be achieved with low cost) Destruction is sometimes involved; checking all is not possible. [Insert Excel Simulation here] Distribution of Means Visual Mean of Means Distribution of Sample Means Many different sample means are possible The sample means cluster closer to the population mean than the population values do. The larger the sample, the closer they cluster around the population mean Therefore the likelihood of a single sample mean being close to the true mean is high Distribution of Sample Means When trying to use a sample to estimate a population mean, we know we won’t get the exact value We want some way of managing the error so as to be as close as we need to be We can decide on a margin of error that we are willing to accept (polls typically 2% - 4%). We cannot eliminate the possibility of getting a value outside that range, but we can keep it small by adjusting the sample size. x How Close Can We Get? The variance of the sample mean is the population variance divided by n (sample size) Thus larger n’s bring smaller variances Let’s look at an example. In order to understand the process, we will assume we actually know the true mean and variance. Each of the following graphs is from a computer simulation of taking 100 samples from a normal population with μ=15 and σ=3, but with different sample sizes. μ=15, σ=3, Sample Size 1 Number observed in [14,16]: 30 30 Percent 20 10 0 7 9 11 13 15 17 s=3 19 21 23 25 μ =15, σ=3, Sample Size 4 Number observed in [14,16]: 52 50 Percent 40 30 20 10 0 7 9 11 13 15 17 s=1.5 19 21 23 25 μ =15, σ=3, Sample Size 9 Number observed in [14,16]: 74 80 70 Percent 60 50 40 30 20 10 0 7 9 11 13 15 17 s=1 19 21 23 25 μ =15, σ=3, Sample Size 16 Number observed in [14,16]: 81 80 70 Percent 60 50 40 30 20 10 0 7 9 11 13 15 17 s=3/4 19 21 23 25 μ =15, σ=3, Sample Size 25 Number observed in [14,16]: 90 90 80 70 Percent 60 50 40 30 20 10 0 7 9 11 13 15 17 s=3/5 19 21 23 25 μ =15, σ=3, Sample Size 36 Number observed in [14,16]: 97 100 90 80 Percent 70 60 50 40 30 20 10 0 7 9 11 13 15 17 s=1/2 19 21 23 25 Number in [14,16] vs Sample Size 100 90 80 70 60 50 40 30 20 10 0 0 5 10 15 20 25 30 35 40 So What? In Real Life, we don’t know the true mean and variance. We want to estimate them. Furthermore, we will only take one sample, which represents just one data point from the distributions we have illustrated. We will probably NEVER know where in the distribution that data point is coming from. Under these conditions, how can we provide an estimate that is trustworthy? Clearly, the sample size directly affects the likelihood that the sample mean will be close to the true mean. Which one would you like to pick from? 100 30 90 80 70 Percent Percent 20 10 60 50 40 30 20 10 0 0 7 9 11 13 15 17 s=3 19 21 23 25 7 9 11 13 15 17 19 21 23 25 s=1/2 The situation: You have 100 balls in an urn (left). Each has an odd number on it, which may be from 7-25, but you don’t know how many of each there are. You will draw one ball and record its number. If this number matches the mean of the distribution, your company will make lots of money and you will get a promotion. However, you have the opportunity, for a sizable fee, to trade in the urn for the one on the right. If you do so, and are wrong, you will be fired because of the excessive expense you incurred. Does the name Pavlov ring a bell? Reading while sunbathing makes you well red. When two egotists meet, it's an I for an I. Notes: 1. x : the sample mean. 2. sx : the standard deviation of the sample means. 3. The theory involved with sampling distributions described in the remainder of this chapter requires random sampling. Random Sample: A sample obtained in such a way that each possible sample of a fixed size n has an equal probability of being selected. (Example: Every possible handful of size n has the same probability of being selected.) The Central Limit Theorem The most important idea in all of statistics. Describes the sampling distribution of the sample mean. Examples suggest: the sample mean (and sample total) tend to be normally distributed. Distribution of Sample Means If all possible random samples of a particular size n are taken from any population with a mean m and a standard deviation s, the distribution of sample means ( x ) will: 1. have a mean m x equal to m. 2. have a standard deviation s x equal to s n . Further, if the sampled population has a normal distribution, then the sampling distribution of x will also be normal for samples of all sizes. Central Limit Theorem The distribution of sample means will come closer to normal as the sample size increases. Graphical Illustration of the Central Limit Theorem: Distribution of x : n = 2 Original Population 10 20 30 x 10 Distribution of x : n = 30 Distribution of x : n = 10 10 x 20 x 10 x Example: Consider a normal population with m = 50 and s = 15. Suppose a sample of size 9 is selected at random. Find: 1. P(45 x 60) 2. P( x 47.5) Solution: Since the original population is normal, the distribution of the sample mean is also (exactly) normal. m x m 50 sx s n 15 9 15 3 5 0.4772 0.3413 45 1 50 0 60 2 45 50 x 50 60 50 P(45 x 60) P 5 5 5 P( 1 z 2) 0.3413 0.4772 0.8185 x z 0.3085 01915 . 47.5 50 .5 0 x 50 47.5 50 P( x 47.5) P 5 5 P( z .5) 0.5000 01915 . 0.3085 x z Example: A report stated that the day-care cost per week in Boston is $109. Suppose we accept this as the true (population) mean cost per week, and also know that the standard deviation is $20. 1. Find the probability that a sample of 50 day-care centers would show a mean cost of $105 or less per week. 2. Suppose the sample of 50 day-care centers results in a sample mean of $120. Does this provide evidence to refute the claim that the true mean is $109? Solution: The shape of the original distribution is unknown, but the sample size, n, is large. The CLT applies. The distribution of x is approximately normal. mx m 109 sx s n 20 50 2.83 0.4207 0.0793 105 141 . 109 0 x 109 105 109 P( x 105) P 2.83 2.83 P( z 141 . ) 0.5000 0.4207 0.0793 x z To investigate the claim, we need to examine how likely a sample mean of $120 is, if the claim is true. Consider how far out in the tail of the sample mean distribution the value $120 is found. Compute the tail probability. x 109 120 109 P( x 120) P 2.83 2.83 P( z 3.89) 0.0001 Since the tail probability is so small, this suggests the observation of $120 is very rare (if the mean cost is really $109). There is evidence to suggest the claim of m = $109 is wrong. In democracy your vote counts. In feudalism your count votes. She was engaged to a boyfriend with a wooden leg but broke it off. A chicken crossing the road is poultry in motion.