* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Chapter 5
Taylor's law wikipedia , lookup
Data mining wikipedia , lookup
Bootstrapping (statistics) wikipedia , lookup
Foundations of statistics wikipedia , lookup
Statistical inference wikipedia , lookup
World Values Survey wikipedia , lookup
History of statistics wikipedia , lookup
Resampling (statistics) wikipedia , lookup
Time series wikipedia , lookup
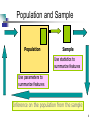
Chapter 5 The Lure of Statistics: Data Mining Using Familiar Tools Note: Included in this Slide Set is a subset of Chapter 5 material and additional material from the instructor. Why a Manager (or you) Needs to Know Some Basics about Statistics • To know how to properly present information • To know how to draw conclusions about populations based on sample information • To know how to improve processes • To know how to obtain reliable forecasts 2 Statistics vs Data Mining • For statisticians, data mining has a negative connotation – one of searching for data to support preconceived ideas • Statistics don’t lie but liars use statistics! • Statistics developed as a discipline to help scientists make sense of observations and experiments, hence the scientific method • Problem has often been too little data for statisticians • DM is faced with too much data • Many of the techniques & algorithms used are shared by both statisticians and data miners 3 Some Definitions • Population (universe) is the collection of things under consideration • Sample is a portion of the population selected for analysis • Statistic is a summary measure computed to describe a characteristic of the sample 4 Some Definitions* • Mean (average) is the sum of the values divided by the number of values • Median is the midpoint of the values (50% above; 50% below) after they have been ordered from the smallest to the largest, or the largest to the smallest • Mode is the value among all the values observed that appears most frequently • Range is the difference between the smallest and largest observation in the sample * laymen’s 5 Population and Sample Population Sample Use statistics to summarize features Use parameters to summarize features Inference on the population from the sample 6 Occam’s Razor – “Kiss” • William of Occam, Franciscan monk, 1280-1349 – prior to modern statistics, the Renaissance and the printing press. • Influential philosopher, theologian, professor with a very simple idea: – Latin: Entia non sunt multiplicanda sine necessitate – English: The simpler explanation is the preferable one or “Keep it simple, stupid!” 7 The Null Hypothesis • The NH assumes that differences among observations are due simply to chance • Bush vs Kerry – poll’s margin of error ~ 3% - 4% • Layperson asks, “Are these %’s different?” • Statistician asks, “What is the probability that these two values are really the same?” 8 Skepticism • Is good for both statisticians and DMiners • Goal for both is to demonstrate results that work, hence discounting the null hypothesis • The less reliance on chance the better 9 P-Values and Q-Values • The null hypothesis can be quantified • The p-value is the probability that the null hypothesis is true • When the null hypothesis is true, nothing is really happening; differences are due to chance • Confidence, the reverse of a p-value, is called the q-value. p-value = 5% then the q-value (confidence) is 95%. • Example: Bush/Kerry…p-value 60% or 5% 10 Data Visualization • Discrete data, such as products, channels, regions, and descriptions is the main focus of data mining • Histogram – bars show number of times different values occur 11 Data Visualization • Histograms describe a single moment in time • Data mining is often concerned with what is happening over time. • Time Series Analysis – choosing an appropriate time frame to consider the data 12 Standardized Values • Time Series charts are useful, but have limitations also; cannot tell whether the changes over time are expected or unexpected • We could look at a segment of the data, say a day at a time asking: “Is it possible that the differences seen on each day are strictly due to chance?” (null hypothesis) • Answer: calculate the p-value for a day 13 Central Limit Theorem • As more and more samples are taken from a population, the distribution of the averages of the samples follows the normal distribution. The average of the samples comes arbitrarily close to the average of the entire population. • Normal distribution is described by the mean (average count) and the standard deviation (clustering around the mean) 14 Different Shapes of Distributions 15 Variance and Standard Deviation • Variance is a measure of the dispersion of a sample (or how closely the observations cluster around the mean [average]) • Standard Deviation, the square root of the variance, is the measure of variation in the observed values (or variation in the clustering around the mean) 16 Example: Sample Scores/Grades • • • • • • • • 84 65 74 72 85 65 96 30 • • • • • • • • • • 78 72 85 64 65 96 15 72 73 85 1. Sort the data from highest to lowest and assign grades 2. Find the Mean, Median, Mode, and Standard Deviation 3. Create a histogram for the grades . 17 Using MS Excel… B Sorted Raw Data 96 96 85 85 85 84 78 74 73 72 72 72 65 65 65 64 30 15 C Grade A A B B B B C C C C C C D D D D F F D (Bx-I5)^2 630.57 630.57 199.12 199.12 199.12 171.90 50.57 9.68 4.46 1.23 1.23 1.23 34.68 34.68 34.68 47.46 1671.90 3123.57 E F G H I Range Mean Median Mode Standard Deviation A's B's C's D's F's W's Sum 81 70.9 72.5 85 19.8 2 4 6 4 2 0 18 18 Using MS Excel… Grade Distribution 7 6 5 4 3 2 1 0 A's B's C's D's F's 19 End of Chapter 5 20