* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Slide 1
Survey
Document related concepts
Transcript
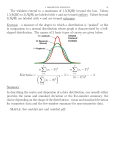
Chapter 1 Measure of Variability Measure of variability • Variability provides a quantitative measure of the degree to which scores in a distribution are spread out or clustered together. • How well does the mean represent the scores in a distribution? The logic here is to determine how much spread is in the scores. • How much do the scores "deviate" from the mean? Think of the mean as the true score or as your best guess. • If every X were very close to the Mean, the mean would be a very good predictor. • If the distribution is very sharply peaked then the mean is a good measure of central tendency and if you were to use the mean to make predictions you would be right or close much of the time. • The larger the standard deviation figure, the wider the range of distribution away from the measure of central tendency Measure of variability 1. Range =Xhighest – Xlowest 2. Quartile: describing a division of observations into four defined intervals based upon the values of the data and how they compare to the entire set of observations. Each quartile contains 25% of the total observations. Generally, the data is ordered from smallest to largest with those observations falling below : -25% of all the data analyzed allocated within the 1st quartile, -50% and allocated in the 2nd quartile, -75% allocated in the 3rd quartile, -and finally the remaining observations allocated in the 4th quartile. 3. Interquartile=Q3-Q1. 4. Semi-interquartile=(Q3-Q1)/2. Measure of variability • Variance –Deviation: deviation of one score from the mean –Variance: taking the distribution of all scores into account. • Standard deviation score 8 25 7 5 8 3 10 12 9 mean deviation* 9.67 - 1.67 9.67 +15.33 9.67 - 2.67 9.67 - 4.67 9.67 - 1.67 9.67 - 6.67 9.67 + .33 9.67 + 2.33 9.67 - .67 sum of squared dev= Standard Deviation = = = = squared deviation 2.79 235.01 7.13 21.81 2.79 44.49 .11 5.43 .45 320.01 Square root(sum of squared deviations / (N-1) Square root(320.01/(9-1)) Square root(40) 6.32 Interquartil • Interquartil (IQR) dirumuskan : IQR = Q3-Q1 • Inner fences & Outer fences IF Q1 1.5( IQR ) & Q3 1.5( IQR ) OF Q1 3( IQR ) & Q3 3( IQR ) Measure of variability Ex Arrange boxplot from the data. Decide if there any outlier! 40, 300, 520, 340, 320, 290, 260, 330 solution MEASURE OF SYMMETRY 1. SKEWNESS Skewness is a measure of symmetry, or more precisely, the lack of symmetry. A distribution, or data set, is symmetric if it looks the same to the left and right of the center point. • SKEWNESS KURTOSIS Kurtosis is a measure of whether the data are peaked or flat relative to a normal distribution. That is, data sets with high kurtosis tend to have a distinct peak near the mean, decline rather rapidly, and have heavy tails. Data sets with low kurtosis tend to have a flat top near the mean rather than a sharp peak. A uniform distribution would be the extreme case. If the skewness is negative (positive) the distribution is skewed to the left (right). Normally distributed random variables have a skewness of zero since the distribution is symmetrical around the mean. Normally distributed random variables have a kurtosis of 3. Financial data often exhibits higher kurtosis values, indicating that values close to the mean and extreme positive and negative outliers appear more frequently than for normally distributed random variables KURTOSIS Exercise 1. Calculate the mean, median, mode, range and standard deviation for the following sample: Midterm Exam X X 100 88 83 105 78 98 126 85 67 88 88 77 114 85 82 96 107 102 113 94 119 91 100 72 88 85 2. Suppose that the following scores were obtained on administering a language proficiency test to ten aphasics who had undergone a course of treatment, and ten otherwise similar aphasics who had not undergone the treatment: Experimental group 15 28 62 17 31 58 45 11 76 43 Control group 31 34 47 41 28 54 36 38 45 32 Calculate the mean score and standard deviation for each group, and comment on the results. Homework I. The following scores are obtained by 50 subjects on a language aptitude test: 42 55 18 61 63 62 27 59 82 25 44 46 58 66 58 32 55 57 80 71 47 47 49 64 82 42 28 55 50 52 52 53 88 40 73 76 44 49 53 67 36 15 50 28 58 43 61 62 63 77 1. Draw a histogram to show the distribution of the scores. 2. Calculate the mean and standard deviation of the scores. 3. Suppose Lihua scored 55 in this test, what’s her position in the whole class? II. Suppose there will be 418,900 test takers for the NMET in 2006 in Guangdong, the key universities in China plan to enroll altogether 32,000 students in Guangdong. What score is the lowest threshold for a student to be enrolled by the key universities? (Remember the mean is 500, standard deviation is 100). Homework Imagine that you received the following data on the vocabulary test mentioned earlier: 20 23 28 30 32 35 22 23 29 30 33 36 23 23 30 30 33 36 23 24 30 31 34 37 23 25 30 32 35 37 1. Chart the data and draw the frequency polygon. 2. Compute the mean, mode, and median of the data and decide which of the three you believe to be best for the central tendency of the data. Homework I. The following are the times (in seconds) taken for a group of 30 subjects to carry out the detransformation of a sentence into its simplest form: 0.55 0.42 0.49 0.72 0.30 0.56 0.41 0.59 0.77 0.32 0.52 0.37 0.75 0.76 0.44 0.59 0.22 0.65 0.39 0.61 0.51 0.24 0.63 0.26 0.54 0.50 0.41 0.61 0.68 0.47 Calculate (i) the mean, (ii) the standard deviation, (iii) the standard error of the mean, (iv) the 99 per cent confidence limits for the mean. II. A random sample of 300 finite verbs is taken from a text, and it is found that 63 of these are auxiliaries. Calculate the 95 per cent confidence limits for the proportion of finite verbs which are auxiliaries in the text as a whole. III. Using the data in question II, calculate the size of the sample of finite verbs which would. be required in order to estimate the proportion of auxiliaries to within an accuracy of 1 per cent, with 95 per cent confidence. Interquartil • Interquartil (IQR) dirumuskan : IQR = Q3-Q1 • Inner fences & Outer fences IF Q1 1.5( IQR ) & Q3 1.5( IQR ) OF Q1 3( IQR ) & Q3 3( IQR ) UKURAN BENTUK • SKEWNESS KURTOSIS Ex Susun boxplot dari data berikut dan tentukan apakah terdapat outlier atau tidak ! Jika ada, tentukan data tersebut dan tentukan apakah outlier atau ekstrem outlier ? 340, 300, 520, 340, 320, 290, 260, 330