Download Slide 1

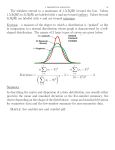
Chapter 1
Measure of Variability
Measure of variability
• Variability provides a quantitative
measure of the degree to which
scores in a distribution are spread
out or clustered together.
• How well does the mean represent the scores in a
distribution? The logic here is to determine how
much spread is in the scores.
• How much do the scores "deviate" from the mean?
Think of the mean as the true score or as your best
guess.
• If every X were very close to the Mean, the mean
would be a very good predictor.
• If the distribution is very sharply peaked then the
mean is a good measure of central tendency and if
you were to use the mean to make predictions you
would be right or close much of the time.
• The larger the standard deviation figure, the wider the range
of distribution away from the measure of central tendency
Measure of variability
1. Range =Xhighest – Xlowest
2. Quartile:
describing a division of observations into four defined
intervals based upon the values of the data and how they
compare to the entire set of observations.
Each quartile contains 25% of the total observations.
Generally, the data is ordered from smallest to largest with
those observations falling below :
-25% of all the data analyzed allocated within the 1st quartile,
-50% and allocated in the 2nd quartile,
-75% allocated in the 3rd quartile,
-and finally the remaining observations allocated in the 4th
quartile.
3. Interquartile=Q3-Q1.
4. Semi-interquartile=(Q3-Q1)/2.
Measure of variability
• Variance
–Deviation: deviation of one score
from the mean
–Variance: taking the distribution of
all scores into account.
• Standard deviation
score
8
25
7
5
8
3
10
12
9
mean
deviation*
9.67
- 1.67
9.67
+15.33
9.67
- 2.67
9.67
- 4.67
9.67
- 1.67
9.67
- 6.67
9.67
+ .33
9.67
+ 2.33
9.67
- .67
sum of squared dev=
Standard Deviation =
=
=
=
squared
deviation
2.79
235.01
7.13
21.81
2.79
44.49
.11
5.43
.45
320.01
Square root(sum of squared deviations / (N-1)
Square root(320.01/(9-1))
Square root(40)
6.32
Interquartil
• Interquartil (IQR) dirumuskan :
IQR = Q3-Q1
• Inner fences & Outer fences
IF  Q1  1.5( IQR ) & Q3  1.5( IQR )
OF  Q1  3( IQR ) & Q3  3( IQR )
Measure of variability
Ex
Arrange boxplot from the data. Decide
if there any outlier!
40, 300, 520, 340, 320, 290, 260, 330
solution
MEASURE OF SYMMETRY
1. SKEWNESS
Skewness is a measure of symmetry, or more precisely,
the lack of symmetry.
A distribution, or data set, is symmetric if it looks the
same to the left and right of the center point.
• SKEWNESS
KURTOSIS
 Kurtosis is a measure of whether the data are peaked or flat
relative to a normal distribution.
 That is, data sets with high kurtosis tend to have a distinct peak
near the mean, decline rather rapidly, and have heavy tails.
 Data sets with low kurtosis tend to have a flat top near the mean
rather than a sharp peak.
 A uniform distribution would be the extreme case.
 If the skewness is negative (positive) the distribution is
skewed to the left (right).
 Normally distributed random variables have a
skewness of zero since the distribution is symmetrical
around the mean.
 Normally distributed random variables have a kurtosis
of 3.
 Financial data often exhibits higher kurtosis values,
indicating that values close to the mean and extreme
positive and negative outliers appear more frequently
than for normally distributed random variables
KURTOSIS
Exercise
1. Calculate the mean, median, mode, range and standard deviation for
the following sample:
Midterm Exam
X
X
100
88
83
105
78
98
126
85
67
88
88
77
114
85
82
96
107
102
113
94
119
91
100
72
88
85
2. Suppose that the following scores were obtained on administering a
language proficiency test to ten aphasics who had undergone a course
of treatment, and ten otherwise similar aphasics who had not
undergone the treatment:
Experimental group
15
28
62
17
31
58
45
11
76
43
Control group
31
34
47
41
28
54
36
38
45
32
Calculate the mean score and standard deviation for each group, and
comment on the results.
Homework
I. The following scores are obtained by 50 subjects on a language aptitude test:
42
55
18
61
63
62
27
59
82
25
44
46
58
66
58
32
55
57
80
71
47
47
49
64
82
42
28
55
50
52
52
53
88
40
73
76
44
49
53
67
36
15
50
28
58
43
61
62
63
77
1. Draw a histogram to show the distribution of the scores.
2. Calculate the mean and standard deviation of the scores.
3. Suppose Lihua scored 55 in this test, what’s her position in the whole class?
II. Suppose there will be 418,900 test takers for the NMET in 2006 in
Guangdong, the key universities in China plan to enroll altogether 32,000
students in Guangdong. What score is the lowest threshold for a student to be
enrolled by the key universities? (Remember the mean is 500, standard
deviation is 100).
Homework
Imagine that you received the following data on the vocabulary test mentioned earlier:
20
23
28
30
32
35
22
23
29
30
33
36
23
23
30
30
33
36
23
24
30
31
34
37
23
25
30
32
35
37
1. Chart the data and draw the frequency polygon.
2. Compute the mean, mode, and median of the data and decide which of the three you
believe to be best for the central tendency of the data.
Homework
I. The following are the times (in seconds) taken for a group of 30 subjects
to carry out the detransformation of a sentence into its simplest form:
0.55
0.42
0.49
0.72
0.30
0.56
0.41
0.59
0.77
0.32
0.52
0.37
0.75
0.76
0.44
0.59
0.22
0.65
0.39
0.61
0.51
0.24
0.63
0.26
0.54
0.50
0.41
0.61
0.68
0.47
Calculate (i) the mean, (ii) the standard deviation, (iii) the standard error
of the mean, (iv) the 99 per cent confidence limits for the mean.
II. A random sample of 300 finite verbs is taken from a text, and it is found
that 63 of these are auxiliaries. Calculate the 95 per cent confidence
limits for the proportion of finite verbs which are auxiliaries in the text
as a whole.
III. Using the data in question II, calculate the size of the sample of finite
verbs which would. be required in order to estimate the proportion of
auxiliaries to within an accuracy of 1 per cent, with 95 per cent
confidence.
Interquartil
• Interquartil (IQR) dirumuskan :
IQR = Q3-Q1
• Inner fences & Outer fences
IF  Q1  1.5( IQR ) & Q3  1.5( IQR )
OF  Q1  3( IQR ) & Q3  3( IQR )
UKURAN BENTUK
• SKEWNESS
KURTOSIS
Ex
Susun boxplot dari data berikut dan
tentukan apakah terdapat outlier atau
tidak ! Jika ada, tentukan data tersebut
dan tentukan apakah outlier atau
ekstrem outlier ?
340, 300, 520, 340, 320, 290, 260,
330