Download Quantitative Measures - University of Oxford

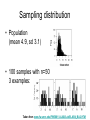
Statistics for Linguistics
Students
Michaelmas 2004
Week 3
Bettina Braun
www.phon.ox.ac.uk/~bettina
Overview
•
•
•
•
•
•
Discussion of last assignment
Z-scores
Sampling distributions
Confidence intervals
Hypothesis testing
Type I and Type II errors
General comments
• Please let every file you submit contain your
initials and the week the assignment was given!
• Please put your name somewhere on the page
• Paste figures into the doc-file (or rtf-file) and only
submit the .sav-files
• Name the x- and y-axis of the figures and give
them a title
• Do not work with var0001 (name and label varia
bles)
• Scale figures so that numbers are readible
Manipulating figures
• If you want to copy SPSS-figures into your
document, it is sensible to increase the
font sizes (otherwise they’ll be too difficult
to read). Also, you might want to change
the title or legend, ...
• Double click on any figure
Measures of central tendency
• Interval data, roughly normally distributed
data (less appropriate for skewed
distributions)
 mean
(although mode and median
should give same results!)
• Interval data, strongly skewed
 mode, median
• Categorical data (different versions, …)
 mode
Sentence lengths
Very likely that most of the sentences do not
exceed 20 to 30 words but there will be few
sentences that are very long…
Sentence length
N.B. It is likely that distribution of sentence lengths in Th. Mann
are skewed to the left…
Preference for 3 resynthesised
versions
• Suppose this were the outcome
version
# subjects
a
20
b
37
c
18
Coding: a=1, b=2, c=3
 mean = 1.97
Mode is more meaningful! If you are reporting a mean,
one might think there is a normal distribution
Merging datasets
Year
1990
1990
1990
1990
…
2000
2000
2000
2000
2000
2000
results
21,00
64,00
48,00
64,00
58,00
33,00
8,00
55,00
47,00
61,00
Year 90
58
59
44
67
50
60
54
…
year 00
30
54
45
67
54
60
45
…
This is how to organise
observations from the same
person in different years
Describe this distribution
25
Frequency
20
15
10
5
Mean = 773,3098
Std. Dev. = 268,96745
N = 163
0
200,00
400,00
600,00
800,00
???
1000,00
1200,00
Normal distribution
(Gaussian distribution)
• Example: IQ scores, mean=100, sd=16
Mean = Median = Mode
z-scores
• Z-score: deviation of given score from the
mean in terms of standard deviations
How likely is a given event?
• Example: time to utter a particular
sentence: x = 3.45s and sd = .84s
• Questions:
– What proportion of the population of utterance
times will fall below 3s?
– What proportion would lie between 3s and
4s?
– What is the time value below which we will
find 1% of the data?
Sample mean and sd as parameter
estimators
• Mean and standard deviation of the
population are unknown
• But we can use the sample mean and sd
as estimators for the parameters of the
unknown population
Sample mean and sd as estimators
Population
parameter
Sample
statistics
mean
Standard
deviation
Degrees of freedom: scores that contain new
information; better estimator for parameter
From sample statistics to
population parameters
• We only know the statistics of our sample
• Sample statistics will differ from population
parameters
• Knowledge about sampling distribution of the
statistic (i.e. how it behaved if large samples
were taken) would tell us how well the statistic
estimated the parameter (degree of confidence)
Sampling distribution
• Population
(mean 4.9, sd 3.1)
• 100 samples with n=50
3 examples:
Taken from www.fw.umn.edu/FW5601/ ALAB/Lab5/LAB4_BA2.HTM
Sampling distribution
• Relative frequency of 100 means:
sample mean: 4.9
sample sd: 0.46
Note:
– Shape of sampling distribution roughly normal
– Mean of sampling distribution is population mean
– Sample sd smaller than population sd
Central limit theorem
Terminology:
n=30
Standard deviation of the sampling distribution
of the means is called standard error of the
mean (SE)
Experimental research
• Often, we are interested if human
behaviour is dependent on certain factors.
E.g.
– Is the speech rate dependent on the dialectal
region?
– Do foreigners and native speakers produce
sentences with the same number of words?
Dependent and independent
variables
• Independent variable:
– Variable(s) manipulated by the experimenter
– experimenter determines the values it will
assume
– Independent variables may have a number of
different levels
• Dependent variable:
– Measure of behaviour (not manipulated or
controlled by experimenter)
Examples
• What are the dependent and independent
variables in the following questions?
– Is the speech rate dependent on the dialectal
region of the speakers?
– Do foreigners and native speakers produce
sentences with the same number of words?
– Is the articulatory precision dependent on the
part-of-speech?
– Do different word orders influence the
grammatiality judgements of subjects?
Null-hypothesis H0
• Generally phrased to negate the possiblity
of a relationship between the independent
and dependent variables
• If the null-hypothesis is true, there is no
interaction between dependent and
independent variables
• Alternative hypothesis contradicts nullhypothesis
Statistical tests of significance
• Allows to evaluate the probability that the
observed sample values would occur if the null
hypothesis were true
• If that probability is sufficiently low, the null
hypothesis can be rejected
• In other words: provide evidence for conlcuding
(with a specified risk of error) that there are or
are no real differences between conditions in the
population
p-value
• Probability that values of the statistic like the one
observed would occur if the null hypothesis were
true
• In other words: how unusual is the observed test
statistic compared to what H0 predicts?
• The smaller p, the more unusual the observed
data if H0 were true
(e.g. p=0.45 very usual, compared to p=0.001)
Type I error
• Type I error:
– Rejection of a true null hypothesis
– That is, in reality, there is no relationship
between independent and dependent variable
but you conclude there is
– Probability of type I error is called α
– α is usually determined before you run an
experiment (often set at 5% or 1%)
Type II error
• Type II error:
– Failure to reject a false null hypothesis
– That is, in reality, there is a relation between
the independent variable and the dependent
one(s) but you conclude there is none
– Probability of type II error is called β
– In contrast to α, β cannot be precisely
controlled
Reducing the Type II error
• β can be reduced by
– Using an α-level of .05 (instead of a more
stringent one)
– Using as many subjects as can be reasonably
obtained
– Selecting the levels of the independent
variable so as to maximise the size of the
effect
– Reducing variability (e.g. controlling more
variables)
Organise SPSS tables
• Every independent variable and every
dependent variable has its own column
• Independent variables are often found before
dependent variables
• It is wise to compare the distributions of the
conditions before statistical tests of significance
(histograms, boxplots)
– Either select the condition you are interested in
– Or split the output according to the different levels
– You can also compare boxplots for the different
conditions
Data exploration
• Error bars show the 95% confidence
interval for the mean (i.e. the mean and
the area where 95% of the data fall in)
Data exploration
• Error bars show the 95% confidence
interval for the mean (i.e. the mean and
the area where 95% of the data fall in)
• One independent variable
– Error bar (simple, groups of variables)
• Two independent variables
– Error bar (clustered, groups of variables)