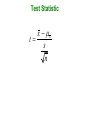Download PowerPoint

8-4 Testing a Claim About a Mean
This section presents methods for testing a claim about a
population mean.
When σ is not known, we use a “t test” that incorporates
the Student t distribution.
Notation
n = sample size
x
= sample mean
 x = population mean
Requirements
1) The sample is a simple random sample.
2) Either or both of these conditions is satisfied:
The population is normally distributed or n > 30.
Test Statistic
x  x
t
s
n
Running the Test
P-values: Use technology or use the Student t
distribution in Table A-3 with degrees of freedom
df = n – 1.
Critical values: Use the Student t distribution with
degrees of freedom df = n – 1.
Important Properties of the
Student t Distribution
1. The Student t distribution is different for different sample
sizes (see Figure 7-5 in Section 7-3).
2. The Student t distribution has the same general bell shape
as the normal distribution; its wider shape reflects the
greater variability that is expected when s is used to
estimate σ.
3. The Student t distribution has a mean of t = 0.
4. The standard deviation of the Student t distribution varies
with the sample size and is greater than 1.
5. As the sample size n gets larger, the Student t distribution
gets closer to the standard normal distribution.
Example
Listed below are the measured radiation emissions (in W/kg)
corresponding to a sample of cell phones.
Use a 0.05 level of significance to test the claim that cell
phones have a mean radiation level that is less than 1.00
W/kg.
0.38
0.55
1.54
1.55
0.50
The summary statistics are:
0.60
0.92
0.96
1.00
0.86
1.46
x  0.938 and s  0.423 .
Example - Continued
Requirement Check:
1. We assume the sample is a simple random sample.
2. The sample size is n = 11, which is not greater than 30, so
we must check a normal quantile plot for normality.
Example - Continued
The points are reasonably close to a straight line and there is
no other pattern, so we conclude the data appear to be from a
normally distributed population.
Example - Continued
Step 1: The claim that cell phones have a mean radiation
level less than 1.00 W/kg is expressed as μ < 1.00 W/kg.
Step 2: The alternative to the original claim is μ ≥ 1.00 W/kg.
Step 3: The hypotheses are written as:
H 0 :   1.00 W/kg
H1 :   1.00 W/kg
Example - Continued
Step 4: The stated level of significance is α = 0.05.
Step 5: Because the claim is about a population mean μ, the
statistic most relevant to this test is the sample mean: x .
Example - Continued
Step 6: Calculate the test statistic and then find the P-value or
the critical value from Table A-3:
x   x 0.938  1.00
t

 0.486
s
0.423
n
11
Example - Continued
Step 7: Critical Value Method: Because the test statistic of
t = –0.486 does not fall in the critical region bounded by the
critical value of t = –1.812, fail to reject the null hypothesis.
Example - Continued
Step 7: P-value method: Technology, such as a TI-83/84 Plus
calculator can output the P-value of 0.3191. Since the P-value
exceeds α = 0.05, we fail to reject the null hypothesis.
Example
Step 8: Because we fail to reject the null hypothesis, we
conclude that there is not sufficient evidence to support the
claim that cell phones have a mean radiation level that is less
than 1.00 W/kg.
Finding P-Values
Assuming that neither software nor a TI-83 Plus calculator is
available, use Table A-3 to find a range of values for the Pvalue corresponding to the given results.
a) In a left-tailed hypothesis test, the sample size is n = 12,
and the test statistic is t = –2.007.
b) In a right-tailed hypothesis test, the sample size is n = 12,
and the test statistic is t = 1.222.
c) In a two-tailed hypothesis test, the sample size is n = 12,
and the test statistic is t = –3.456.
Example – Confidence
Interval Method
We can use a confidence interval for testing a claim about μ.
For a two-tailed test with a 0.05 significance level, we
construct a 95% confidence interval.
For a one-tailed test with a 0.05 significance level, we
construct a 90% confidence interval.
Example – Confidence
Interval Method
Using the cell phone example, construct a confidence interval
that can be used to test the claim that μ < 1.00 W/kg,
assuming a 0.05 significance level.
Note that a left-tailed hypothesis test with α = 0.05
corresponds to a 90% confidence interval.
Using methods described in Section 7.3, we find:
0.707 W/kg < μ < 1.169 W/kg
Example – Confidence
Interval Method
Because the value of μ = 1.00 W/kg is contained in the
interval, we cannot reject the null hypothesis that μ = 1.00
W/kg .
Based on the sample of 11 values, we do not have sufficient
evidence to support the claim that the mean radiation level is
less than 1.00 W/kg.