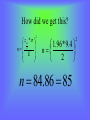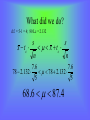Download Confidence Intervals

Confidence Intervals
Week 10
Chapter 6.1, 6.2
What is this unit all about?
• Have you ever estimated something and
tossed in a “give or take a few” after it?
• Maybe you told a person a range in which
you believe a certain value fell into.
• Have you ever see a survey or poll done,
and at the end it says: +/- 5 points.
• These are all examples of where we are
going in this section.
Chapter 6.1 - disclaimer
• To make this unit as painless as possible, I will
show the formula but will teach this unit with
the use of the TI – 83 graphing calculator
whenever possible.
• It is not always possible to use the TI-83 for
every problem.
• You can also follow along in Chp. 6.1 in the
TEXT and use their examples in the book to
learn how to do them by hand.
What is a Confidence Interval?
• If I were to do a study or a survey, but could
not survey the entire population, I would do
it by sampling.
• The larger the sample, the closer the results
will be to the actual population.
• A confidence interval is a point of estimate
(mean of my sample) “plus or minus” the
margin of error.
What will we need to do these?
• Point of estimate – mean of the random
sample used to do the study.
• Confidence Level – percentage of accuracy
we need to have to do our study.
• Critical two-tailed Z value - (z-score) using
table IV.
• Margin of Error – a formula used involving
the Z value and the sample size.
Formula for Confidence Intervals
* This formula is to be used when the Mean and
Standard Deviation are known:
x  z 

2
n
   x  z 
x  samplemean
n  samplesize
  populationmean
2
z 
2

n

n
 m arg inoferror
Finding a Critical Z-value
(Ex 1) – Find the critical two-tailed z value
for a 90% confidence level:
* This means there is 5% on each tail of the
curve, the area under the curve in the
middle is 90%. Do Z (1-.05) = Z .9500
*We will be finding the z score to the left of
.9500 in table IV. It lands in-between
.9495-.9505, thus it is = +/- 1.645
(this is the 5% on each end)
Finding a Critical Z-value
(Ex 2) – Find the critical two-tailed z value
for a 95% confidence level:
* This means there is 2.5% on each tail of the
curve, the area under the curve in the
middle is 95%. Do Z (1-.025) = Z .9750
*We will be finding the z score to the left of
.9750 in table IV.
* It is = +/- 1.96
(this is the 2.5% on each end)
Finding a Critical Z-value
(Ex 3) – Find the critical two-tailed z value
for a 99% confidence level:
* This means there is .005% on each tail of
the curve, the area under the curve in the
middle is 99%. Do Z (1-.005) = Z .9950
*We will be finding the z score to the left of
.9950 in table IV.
* It is = +/- 2.575
(this is the .005% on each end)
Finding a Critical Z-value
(Ex 4) – Find the critical two-tailed z value
for a 85% confidence level:
Margin of Error
  
E  Z   

n
2 
• The confidence interval is the sample mean,
plus or minus the margin of error.
Find the MoE:
Ex (5) – After performing a survey from a
sample of 50 mall customers, the results had
a standard deviation of 12. Find the MoE
for a 95% confidence level.
Special features of Confidence Intervals
As the level of confidence (%) goes up, the
margin of error also goes up!
As you increase the sample size, the margin of
error goes down.
To reduce the margin of error, reduce the
confidence level and/or increase the sample size.
 If you were able to include the ENTIRE
population, the would not be a margin of error.
The magic number is 30 samples to be
considered an adequate sample size.
Finding Confidence Intervals:
(Ex 6) – After sampling 30 Statistics students
at NCCC, Bob found a point estimate of an
81% on Test # 3, with a standard deviation
of 8.2. He wishes to construct a 90%
confidence interval for this data.
How did we get that?
x  z 
2

n
   x  z 
2

n
8.2
8.2
81  1.645 
   81  1.645 
30
30
78.5    83.5
Using TI-83 to do this:
•
•
•
•
Click STAT
go over to TESTS
Click ZInterval
Using the stats feature, input S.D., Mean,
sample size, and confidence level.
• arrow down, and click enter on calculate.
Finding Confidence Intervals:
(Ex 7) – After sampling 100 cars on the I-90,
Joe found a point estimate speed 61 mph
and a standard deviation of 7.2 mph. He
wishes to construct a 99% confidence
interval for this data.
Finding an appropriate sample size
• This will be used to achieve a specific
confidence level for your study.
 z *
 2
n
 E






2
Find a sample size:
(Ex 8) – Bob wants to get a more accurate idea of
the average on Stats Test # 3 of all NCCC stats
class students . How large of a sample will he
need to be within 2 percentage points (margin
of error), at a 95% confidence level, assuming
we know the σ = 9.4?
How did we get this?
 z *
 2
n
 E






2
 1.96 * 9.4 
n

2


n  84.86  85
2
Finish Bob’s Study:
Ex (9) - Now lets say Bob wants to perform
his study, finds the point of estimate for
Test # 3 = 83, with a SD of 9.4 and
confidence level of 95%. Find the
confidence interval for this study.
x  z 
2

n
   x  z 
2

n
What about an interval found with
a small sample size? (chp 6.2)
To do these problems we will need:
TABLE 5: t-Distribution.
Determine from the problem: n, x, s.
Sample, mean, sample standard deviation.
Use the MoE formula for small samples:
E  tc
s
n
tc  t-value from Table 5
d.f. = n-1
(degrees of freedom)
Small Sample Confidence Int.
(Ex 10) – Trying to determine the class
average for Test # 3, Janet asks 5 students
their grade on the test. She found a mean of
78% with a σ = 7.6. Construct a confidence
interval for her data at a 90% confidence
level.
What did we do?
d.f. = 5-1 = 4; .90 Lc = 2.132
s
s
x  tc 
   x  tc 
n
n
7.6
7.6
78  2.132 
   78  2.132 
5
5
68.6    87.4
Or with TI-83/84
STAT
TESTS
8:TInterval
Stats
Input each value, hit calculate.