Download Lecture 1

Course Review
15-211
Fundamental Structures
of Computer Science
Ananda Guna
May 04, 2006
This course was about
How to solve computing problems
using:
• Problem analysis, to abstract away details
and divide into smaller subproblems.
• Mathematical foundations for precise
formulations of problems and solutions.
• Data structures and algorithms to solve
problems correctly and efficiently.
• Java programming and modular software
construction for good implementations.
Data Structures/Algorithms
-Complexity
big-O, little-O, Omega etc..
-Lists
- linked, doubly, singly, multi-linked
- Trees
- general, B-trees, BST, splay, AVL, etc.
- Stacks and Queues
- operations, analysis
- Heaps
- binary, binomial
- Hash Tables
. - collisions, implementation
- Graphs
- traversals, shortest paths
- FSM
- regular expressions, KMP
- String Matching
- KMP, Boyer-Moore, Rabin-Karp
Data Structures/Algorithms
- Dynamic Programming
- table(bottom-up), recursion(top-down)
- memoization
- Game Trees
- mini-max, alpha-beta, iterative deepening
- Sorting
bubble, quick, insertion, selection
-Algorithms
-findMax, findMedian, reverse, MST, compression
-Traversals, shortest path
Java Programming
Object oriented programming.
Correctness (loop invariants, induction).
Time and space complexity.
Debugging (test harness).
Studying for the Final Exam
Review all material first
• Lectures, programs, quizzes
Do sample finals – under time
restrictions.
Old finals are in blackboard/course
material
Types and difficulty of problems may
be similar (some topics not covered)
Complexity
Complexity
Upper and lower bounds
f(n)=n2
T(N) = O(f(N))
T(N) = (g(N))
cf(N)
T(N)
dg(N)
N
f(n) is O(g(n)) iff
f(n) is o(g(n)) iff
f(n) is Ω(g(n)) iff
f(n) is θ(g(n)) iff
g(n) = n
h(n) = log n
Complexity
True or False? If true prove it, else give counter example
Space Complexity
How much memory is needed to run the program
• quicksort
• merge Sort
• insertion sort
• Prim’s
• Dijkstra’s
Key Point: consider the sizes of the data structures used
Solving Recurrences, Asymptotics
Solve T(n) = 3 T(n/3) + 1
Prove the correctness
• By induction
• Invariants
 Hold initially
 Preserved after each iteration of loop or
method call
• Or other methods
Complexity
A is an array of integers
Complexity of known algorithms
Algorithm
Complexity(runtime)
Bubble sort
O(n2) – average, worst, O(n) – best
Insertion sort
O(n2) – average, worst, O(n) – best
Selection sort
O(n2) – average, worst, best
Find Max, Find min
O(n), cannot be done in o(n)
Find Median
With sorting O(n*logn)
Quick sort
but O(n) using quick select
O(nlogn) – average & best, O(n2) – worst
Merge Sort
O(nlogn) – average, best, worst
Heap Sort
O(nlogn) – best, worst, average
Build heap
O(n)
Complexity of known algorithms
Algorithm
Complexity
Heap – find min
O(1)
Heap – delete Min
O(logn)
Heap -insert
O(logn)
Hash – insert, find,
delete
Graph - build
O(1)
Graph - Traverse
O(V2) – space (adjacency matrix)
O(V+E) – space (adjacency list)
O(E)
Graph – Topological
Sort
Graph – Dijkstra’s
O(V + E)
MST – prim’s
O(E+V2)
O((E+V) logE)
Complexity of known algorithms
Algorithm
MST – Kruskal’s
Dynamic
Programming
Complexity
O(E logE) – sort the edges
O(V logV) – find and union operations
O(Table size)
Disjoint sets - union
Linear with memoization
O(logn)
Disjoint sets - find
O(logn)
KMP
O(n+m)
Sorting
Sorting and lower bounds
Insertion Sort
Selection Sort
Heapsort
Mergesort
Quicksort
Radix Sort
Sorting and lower bounds
N2 vs Nlog N
Quicksort idea
 Choose a pivot.
N^2
Nlog N
Upper and lower bounds
T(N) = O(f(N))
T(N) = (g(N))
 Rearrange so that
pivot is in the
“right” spot.
 Recurse on each
half and conquer!
cf(N)
T(N)
dg(N)
N
Questions
Trees
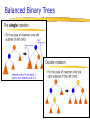
Balanced Binary Trees
AVL Trees
1. Traverse the tree inorder
2. Do exactly two rotations so that
the tree is balanced
3. Consider a binary tree of height h
a. What are the max and min number
of nodes?
b. What are the max and min number
of leaves?
4. Perfect, full, complete trees
Splay Trees
Full, Complete and Perfect Trees
Definitions
Full, complete and perfect
Ex: Show that a full binary tree with n leaves has (n-1) internal
nodes. (use induction on n) Therefore a full binary tree with n
leaves has (2n-1) nodes
Ex: Start from the root and do a preorder traversal as follows. Write
1 for a node with 2 children. Visit left child, then right child.
Write 0 if the node is a leaf. Therefore a full binary tree with 3
nodes can be represented by bit sequence 100.
What is the bit sequence representing a full binary tree with 8
leaves?
Code Examples
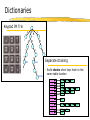
Dictionaries
Dictionaries
Keypad IM Trie
4
5
9
…
I
4
6
6
5
3
8
8
3
like
you
Separate chaining
love
5
…
9
lovely
 Build chains when keys hash to the
same table location
0
1
2
3
4
5
6
7
8
9
10
11
12
As
with
long
key
int
hash
foo
foo
link
char
url
open
list
in
onto
type
queue
test
info
fail
find
Hashing
Describe why hashing a string to sum
of its characters is not a good idea.
Assume S = a1a2….an is a string
Define H(S) =  ai2i-1 (i=1..n)
Describe a way to efficiently calculate
H(S)
Heaps
Priority Queues and Heaps
Suppose you implement a priority
queue using following
• Unsorted array
• Linked list (smallest at front)
• Heap
What is the complexity in each case
for
• deleteMin
• insert
Binary heaps
Representing complete binary trees
• Arrays (1-based)
 Parent at position i
 Children at 2i (and 2i+1).
1 2 3
4 5 6 7
8 9 10
1
2
4
8
5
9
Percolation down
3
10
6
7
• Bubble the transplanted leaf value down
the tree until the heap order property is
satisfied.
1
2
-14
16
24
21
65 26
32 31
19 68
31
14
24
65 26
16
21
32
19 68
Compression
Compression
Compare two images
Binary LZW: Compression example
10010110011
^
Input:
0
Dictionary:
0
1
0
1
1
1
0
0
One image is 400K the other is 1100K. Which is which?
2
1
Tree representation
3
0
4
Output:
1034
1
5
• Represent prefix free
codes as full binary trees
0
• Full: every node
 Is a leaf, or
 Has exactly 2 children.
• The encoding is then a
(unique) path from the
root to a leaf.
0
0
c
1
a
1
d
1
b
a=1, b=001, c=000, d=01
LZW compression
Binary LZW: Compression example
10010110011
^
Input:
0
Dictionary:
0
1
0
1
1
1
0
0
2
1
3
0
4
Output:
1034
1
5
Data Compression
Encode “I AM SAM SAM I AM SAM SAM”
using
• Huffman compression
• LZW
• In each case calculate the compression ratio
Is it possible to apply Huffman after
applying LZW?
If so apply Huffman to output generated
by LZW above
Graphs
Graphs
Adjacency lists and matrices
Traversal (DFS, BFS)
Reachability (DFS, BFS, Warshall)
Shortest Paths (Dijkstra, BellmanFord)
MST (Prim, Kruskal)
Graphs
What is breadth first traversal(BFS)?
What is depth first traversal(DFS)?
What data structures can be used to
implement each one?
Reachability
Connected components
Topological sort
Graphs
Dijkstra’s algorithm
2
f
c
4
2
1
s
2
4
b
5
a
e
1
1
g
d
a e f g
4 6 6 
Visited
s (D = 0)
b (D = 2)
d (D = 3)
c (D = 4)
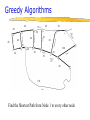
Greedy Algorithms
60
40
60
20
50
40
40
40
50
50
60
10
20
20
100
20
30
50
40
150
Find the Shortest Path from Node 1 to every other node
Dijkstra’s Algorithm
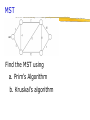
MST
Find the MST using
a. Prim’s Algorithm
b. Kruskal’s algorithm
Homework
1. A graph G is bipartite if the vertex set V can be
partitioned into two subsets L and R, such that
every edge has one vertex in L the other in R.
Give an example of a bipartite graph.
2. G is a tree if it is connected and acyclic. What is
the number is edges in a tree with n nodes?
3. Draw all possible connected graphs G on 4
vertices and 3 edges.
4. Draw all possible connected graphs G on 4
vertices and 4 edges.
5. Suppose G is not connected. What the maximum
number of edges in G?
5. Prove or give a counterexample to the following
claim: Any tree is bipartite.
Dynamic Programming
Dynamic Programming
Dependent subproblems, recursive
solutions, memoizing, explicit tables.
Knapsack
Longest Common Subsequence
Matrix Multiplication
Game Trees
Game trees
A Tic Tac Toe Game Tree
moves
moves
moves
Games
2-person, deterministic, complete
information, ...
Backtracking
MiniMax
Alpha-beta pruning
Heuristics, iterative deepening, move order,
tricks, ...
Disjoint Sets
Union-find
Union, v.0
1
3
2
 {1,2}{0,3}{4}{5}
{1,2,0,3}{4}{5}
1
 union(0,2)
s: 3 -1 1 -1 -1 -1
s’: 3 -1
0
1
1
2
1 -1 -1
3
4
5
4
5
0
2
4
3
5
0
before
after
public void union(int x, int y){
s[find(x)] = find(y);
}
Trick 2: Path compression
 find flattens trees
• Redirect nodes to point directly to the root
 Example: find(0)
1
2
4
3
5
1
2
3
0
4 5
0
 Do this whenever traversing a path from
node to root.
Regular Expressions
Exercises
Homework
Write a regular expression of the alphabet {a, b,
c, d} that describes all strings consisting of
either an odd number of a's or an even number
of b's, followed by any number (and ordering) of
c's and d's. Zero is an even number and any
number of x's can be zero x's. Draw a FSM to
recognize any such string
String matching
Final Exam
Monday, May 8, 8:00 –11:00 am
Make sure not to be late.
Final Exam
Closed book, no calculators, cell
phones, pagers, IM, …
You can bring 1 (one) page of notes.
Bring fluids
Conclusion
Review all material
Do all sample quizzes and finals
Good luck!!