* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Powerpoint - MHS Comp Sci
Survey
Document related concepts
Transcript
Heaps and Priority Queues v2
Starring: Min Heap
Co-Starring: Max Heap
1
Purpose:
In this lecture we will discuss the Priority
Queue ADT , the Java PriorityQueue
Class and a Heap implementation of a
priority Queue
2
Resources:
Java Methods AB Data Structures Chapter 7
p.175
Java Essentials Study Guide Chapter 17 .7/8
p.330 & Chapter 20.1 p.398 & Chapter 20A.4/5
p.418
Barrons Chapter 9 p.305 & Chapter 12 p.414
AP Java Text Chapter 19.7 p.843 & Chapter
21.4 p.950
3
Handouts:
1.
Priority Queue Class
CODE:
PQ.java
PriorityString.java
PriorityQueueExample.java
Jobs.java
4
Intro:
So far we have seen data structures that
maintain and process data in the following
ways:
Store data in order based on a Key
Store data in order based on the “value” of
the object
Store data in order of arrival
Store data in reverse order of its arrival
Store data in random order
5
There are times when we need to maintain and
process data based on their relative importance
or Priority
6
For example, people waiting to but concert
tickets. The priority of the order they are
allowed to purchase tickets is based on the
number on a wrist band that are distributed.
The number on the wristband determines when
they get served
7
If you go to an amusement park, you can select
a predetermined time to get on an attraction.
When the time comes, you get into a Priority
Queue which gets processed first
8
In a hospital emergency room, a triage system
identifies the urgent patients all of whom are
seem before the normal patients regardless
of their order of arrival
9
In operating systems, jobs are processed based
on a specific priority so that a recently
submitted job with a high priority will process
before lower priority jobs even though these
jobs were in the queue longer
10
What we Will Cover in This Lecture:
Priority Queue ADT
Priority Queue Java Class
Priority Queue Implementations
Heap Implementation
The AP AB Requirements
11
Priority Queue ADT
PQ’s Support functionality that maintains a large
set of elements that are ranked in some way
and to have quick access to the HIGHEST
ranked element
12
Priority Queue ADT
PQ is a collection of the same type object
values
These object values contain data and a priority
These objects are ordered in a way that allows
the HIGHEST priority item to be removed first
13
Example of a priority queue where items entered have a priority of 1,2 or 3:
EMPTY PQ
(ADD)
A (2)
B (2) A (2)
C (2) B (2) A (2)
(REMOVE MIN)
C (2) B(2)
(ADD)
D (3) C (2) B(2)
(REMOVE MIN)
D (3) C (2)
(ADD)
E (1) D (3) C (2)
F (1) E (1) D (3) C (2)
(REMOVE MIN)
F (1) D (3) C (2)
D (3) C (2)
D (3)
EMPTY PQ
14
If several items maintain the same
priority then the first one in the queue
is processed first
15
Priority Queues Must Provide for the adding
and removing of elements in a way that
ensures the HIGHEST Priority Item is
removed First
Here is the Priority Queue Java Class:
16
public Class PriorityQueue
{
boolean isEmpty()
boolean add(E x)
E remove ()
E peek ()
Iterator E iterator()
}
17
import java.util.PriorityQueue;
SPVM
PriorityQueue<String> P = new
PriorityQueue<String>(10);
P.add("Sally");
P.add("Betty");
P.add("Xavier");
P.add("Teresa");
P.add("David");
18
if(P.isEmpty())
{
System.out.println("QUEUE EMPTY");
}
else
{
System.out.println(P.size());
}
P.remove();
System.out.println(P.peek());
19
Iterator i = P.iterator();
i = P.iterator();
while(i.hasNext())
{
System.out.println(i.next());
}
System.out.println();
for(String x:P)
{
System.out.println(x.toString());
}
20
The priority of each item in the queue is
established using the Comparable
interface
Every time the remove or peek method
is executed the SMALLEST element
with respect to the compareTo method
is returned
21
Other Priority Queue Implementations
You are required to know Java’s PQ
implementation as well as to understand their
general principles that require any Data
Structure to allow for:
Quick insertion of PQ elements
Quick retrieval of an element with the top priority
Potential PQ implementations include:
22
Linked List where new nodes are inserted
at the front of the list O(1) and the
removal searches the list for the highest
priority node O(n)
23
Linked List where nodes are inserted in
priority order with the smallest elements in
the front nodes O(n) and removal simply
unlinks the front node O(1)
24
Array with nodes inserted at the end of
the List O(1) and removals search for
the highest priority element O(n)
25
A sorted Array where the highest priority
elements (smallest values) are added at
the end of the List O(n) and removal
takes off he last element in the array O(1)
26
TreeSet where adding an element is
O(Log N) and Removal is O(Log N)
27
Heap Implementation
The most common implementation of a PQ is a
Binary Heap
With a PQ we use a Minimum Heap
With these type of heaps the VALUE of every
node is LESS THAN or EQUAL to that of its
children
28
A HEAP is viewed as a Complete Binary
Tree where there are no GAPS at any
level.
The Last level may have some leaves
missing on the right, but every node
except the last must have a node after it.
The nodes are in the leftmost positions
29
Each addition to the heap MUST maintain
the property where the parent node is at
least as small as its children
30
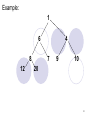
Example:
1
6
8
12
4
7
9
10
20
31
The lower the number, the higher the
priority
The element with the HIGHEST priority is
kept at the root so removing an element
requires removal of the root and then
restructuring of the heap
32
ReHeaping is a O(LogN) operation
Inserting into the heap also requires
Reheaping and is O(LogN)
ALL elements added to a PQ must
implement the Comparable interface and
be of the same class
33
Inserting and Removing elements
to the Heap
34
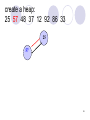
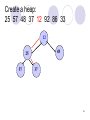
create a heap:
25 57 48 37 12 92 86 33
25
35
create a heap:
25 57 48 37 12 92 86 33
25
57
36
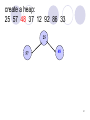
create a heap:
25 57 48 37 12 92 86 33
25
57
48
37
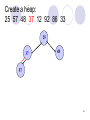
Create a heap:
25 57 48 37 12 92 86 33
25
37
48
57
38
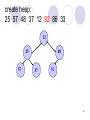
Create a heap:
25 57 48 37 12 92 86 33
12
48
25
57
37
39
create heap:
25 57 48 37 12 92 86 33
12
25
57
48
37
92
40
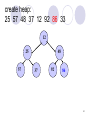
create heap:
25 57 48 37 12 92 86 33
12
25
57
48
37
92
86
41
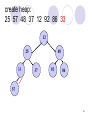
create heap:
25 57 48 37 12 92 86 33
12
25
33
48
37
92
86
57
42
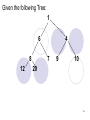
Given the following Tree:
1
6
8
12
4
7
9
10
20
43
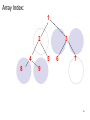
Match this heap with an indices of an Array:
Heap Priority
1
6
4
8
7
9
10
12
20
Array Element (IGNORE
ZERO)
0
1
2
3
4
5
6
7
8
9
44
Array Index:
1
2
4
8
3
5
6
7
9
45
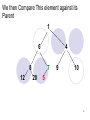
Lets Insert an element with a priority of 5
We insert the new element in the next open
slot ( index 10 or left child of element with
Priority of 7)
46
We then Compare This element against its
Parent
1
6
4
8
12
7
20
9
10
5
47
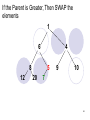
If the Parent is Greater, Then SWAP the
elements
1
6
4
8
12
5
20
9
10
7
48
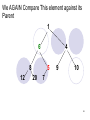
We AGAIN Compare This element against its
Parent
1
6
4
8
12
5
20
9
10
7
49
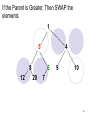
If the Parent is Greater, Then SWAP the
elements
1
5
4
8
12
6
20
9
10
7
50
Again We Compare This Element against its
New Parent
But since the Parent is SMALLER than the
this element, we are done RE-HEAPING
The order of the Heap is maintained as all
children are LARGER than their parent
51
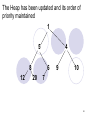
The Heap has been updated and its order of
priority maintained
1
5
4
8
12
6
20
9
10
7
52
We can implement a Heap as a Binary Tree
but it is more efficient to implement a Binary
Heap as an Array
Using your own array or the ArrayList
53
Non-Linked Representation of Binary Trees is a
more efficient way of implementing heaps.
Here all nodes are stored in an array in a
certain order so that for each node it is easy to
find its children and its parent
54
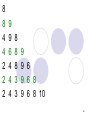
EXAMPLE:
Given the previous PQ, the following is the
construction of the array at each stage of
insertion:
8 9 4 6 2 3 10
55
8
8
4
4
2
2
2
9
9
6
4
4
4
8
8
8
3
3
9
9 6
9 6 8
9 6 8 10
56
If you match the element number,
starting at element 1, with the Binary
Heap, you will see an exact
correlation
57
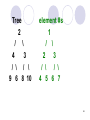
Tree
2
/ \
4
3
/ \ / \
9 6 8 10
element #s
1
/ \
2
3
/ \
/ \
4 5 6 7
58
Each level contains twice as many nodes as the
preceding level.
59
The left and right children of the
i-th node, if they are present, have
the numbers 2i and 2i+1 and its
parent has the number i/2
(truncated to an integer)
60
Using this algorithm, we can manipulate
an array as a Binary HEAP
61
REMEMBER THAT A COMPLETE TREE is a
tree where there are no GAPS at any level.
The Last level may have some leaves
missing on the right, but every node except
the last must have a node after it.
The nodes are in the leftmost positions
62
A Complete Tree
63
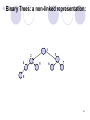
Binary Trees: a non-linked representation:
1
3
2
4
5
6
7
8
64
This property allows us to store a
complete tree in an array where the
element x[n] corresponds to node
number n
Count the elements of the array
starting from element 1 (leave
element 0 unused)
65
Heap remove deletes an element from the
root of the heap
Then the heap needs to be adjusted to preserve
its ordering property and to keep it a complete
tree.
Remove the root (first element in the heap)
66
Place the last element of the heap into
its root (first element). This is the
RIGHTMOST node in the lowest tree level
Then move down from level to level,
swapping it with its smaller child until it
falls into place
67
This process is called the REHEAP
DOWN procedure
68
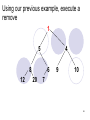
Using our previous example, execute a
remove
1
5
4
8
12
6
20
9
10
7
69
We take the last element in the heap (10th
index / value #7) and move it to the top of
the heap
Then swap this element with its smaller
child Swap #7 with #4
Continue this until this node is smaller
than its children
70
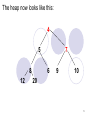
The heap now looks like this:
4
5
8
12
7
6
9
10
20
71
We can also have a Maximum Heap
where all elements are Stored with the
HIGHEST value at the top of the heap
Here, all parents have a HIGHER value
than their children
72
Here element x[1] of the array
corresponds to the root of the heap.
Example:
55 21 34 3 8 13 5 1 2 1
queued items
73
TREEVIEW:
1
55
3
2
34
21
4
5
3
8
7
6
13
5
9
1
8
2
1
10
74
ARRAYVIEW: Element #
0
1
2
3
4
5
6
7
8
9
10
Value
unused
55
21
34
3
8
13
5
1
2
1
75
Priority Queues maintain data as well as a
priority
You can create a class that serves as the
“element” that is stored in the Heap
76
In the PriorityString class there is a data
part and an Integer that represents the
objects priority
The SMALLER the number the HIGHER
the priority
77
Lets look at the PriorityString.java class in
the handout
78
The ArrayPriorityQueue.java class
implements the Priority Queue as an
ArrayList
79
Lets look at the ArrayPriorityQueue.java
class in the handout
80
Finally, to put it all together we use our
Array Priority Queue in a Driver Program
Lets look at PriorityQueueExample.java in our
handout
81
RUN the Priority
QueuesAndExamples.java
RUN and Review the program
JOBS.JAVA
82
AP AB Subset Requirements
Students are expected to:
Understand the PQ ADT & Use Java’s PQ
How the PriorityQueue can be implemented
(insert, remove, peek, reheap) in other ways
than the Java Class
Create a Class that is used as the element of
a PQ
Utilize a PQ implementation in a Driver
83
LABS:
Write a Heap Class
Social Security Administration
Multiple Choice from Barrons:
Chapter 9 p.317 #s 14 to 18
84