* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download ppt
Survey
Document related concepts
Transcript
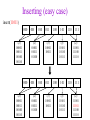
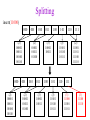
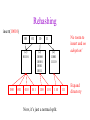
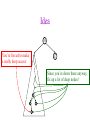
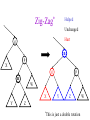
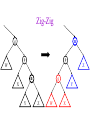
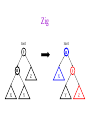
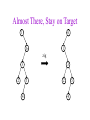
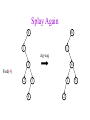
CSE 326: Data Structures Lecture #13 Extendible Hashing and Splay Trees Alon Halevy Spring Quarter 2001 Extendible Hashing • Hashing technique for huge data sets – optimizes to reduce disk accesses – each hash bucket fits on one disk block – better than B-Trees if order is not important • Table contains – buckets, each fitting in one disk block, with the data – a directory that fits in one disk block used to hash to the correct bucket Extendible Hash Table • Directory contains entries labeled by k bits plus a pointer to the bucket with all keys starting with its bits • Each block contains keys+data matching on the first j k bits directory for k = 3 000 (2) 00001 00011 00100 00110 001 (2) 01001 01011 01100 010 011 (3) 10001 10011 100 101 (3) 10101 10110 10111 110 111 (2) 11001 11011 11100 11110 Inserting (easy case) insert(11011) 000 (2) 00001 00011 00100 00110 010 (2) 01001 01011 01100 000 (2) 00001 00011 00100 00110 001 001 (2) 01001 01011 01100 011 100 (3) 10001 10011 010 011 (3) 10001 10011 101 110 (3) 10101 10110 10111 100 101 (3) 10101 10110 10111 111 (2) 11001 11100 11110 110 111 (2) 11001 11011 11100 11110 Splitting insert(11000) 000 (2) 00001 00011 00100 00110 000 (2) 00001 00011 00100 00110 001 010 (2) 01001 01011 01100 001 (2) 01001 01011 01100 010 011 (3) 10001 10011 011 100 (3) 10001 10011 100 101 110 (3) 10101 10110 10111 101 (3) 10101 10110 10111 110 111 (2) 11001 11011 11100 11110 111 (3) 11000 11001 11011 (3) 11100 11110 Rehashing insert(10010) 00 01 (2) 01101 000 001 010 10 (2) 10000 10001 10011 10111 011 100 No room to insert and no adoption! 11 (2) 11001 11110 101 110 Now, it’s just a normal split. 111 Expand directory Rehash of Hashing • Hashing is a great data structure for storing unordered data that supports insert, delete, and find • Both separate chaining (open) and open addressing (closed) hashing are useful – separate chaining flexible – closed hashing uses less storage, but performs badly with load factors near 1 – extendible hashing for very large disk-based data • Hashing pros and cons + very fast + simple to implement, supports insert, delete, find - lazy deletion necessary in open addressing, can waste storage - does not support operations dependent on order: min, max, range Recall: AVL Tree Dictionary Data Structure • Binary search tree properties 8 – binary tree property – search tree property 5 11 • Balance property – balance of every node is: -1 b 1 – result: • depth is (log n) 2 6 4 10 7 9 12 13 14 15 Splay Trees “blind” rebalancing – no height info kept • amortized time for all operations is O(log n) • worst case time is O(n) • insert/find always rotates node to the root! – Good locality – most common keys move high in tree Idea 10 You’re forced to make a really deep access: 17 Since you’re down there anyway, fix up a lot of deep nodes! 5 2 9 3 Splay Operations: Find • Find(x) 1. do a normal BST search to find n such that n->key = x 2. move n to root by series of zig-zag and zig-zig rotations, followed by a final zig if necessary * Zig-Zag Helped Unchanged Hurt g n p X g p n W X Y Y Z Z *This is just a double rotation W Zig-Zig n g p p W Z n g X Y Y Z W X Zig root p root n n p Z X Y X Y Z Why Splaying Helps • Node n and its children are always helped (raised) • Except for final zig, nodes that are hurt by a zigzag or zig-zig are later helped by a rotation higher up the tree! • Result: – shallow (zig) nodes may increase depth by one or two – helped nodes may decrease depth by a large amount • If a node n on the access path is at depth d before the splay, it’s at about depth d/2 after the splay – Exceptions are the root, the child of the root, and the node splayed Locality • Assume m n access in a tree of size n – Total amortized time O(m log n) – O(log n) per access on average • Gets better when you only access k distinct items in the m accesses. – Exercise. Splaying Example 1 1 2 2 zig-zig 3 3 Find(6) 4 6 5 5 6 4 Still Splaying 6 1 1 2 6 zig-zig 3 3 6 5 4 2 5 4 Almost There, Stay on Target 1 6 6 1 zig 3 2 3 5 4 2 5 4 Splay Again 6 6 1 1 zig-zag 3 4 Find(4) 2 5 4 3 2 5 Example Splayed Out 6 4 1 1 6 zig-zag 3 4 3 2 5 2 5 Splay Tree Summary • All operations are in amortized O(log n) time • Splaying can be done top-down; better because: – only one pass – no recursion or parent pointers necessary • Invented by Sleator and Tarjan (1985), now widely used in place of AVL trees • Splay trees are very effective search trees – relatively simple – no extra fields required – excellent locality properties: frequently accessed keys are cheap to find Coming Up • Project 3: implement a “smart” web server. • Heaps! • Disjoint Sets • Graphs and more.