Download 19-TreeIntroBST

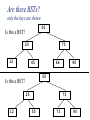
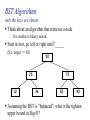
Chapter 18
Binary Trees
Data Structures and Design in Java
© Rick Mercer
A 3rd way to structure data
 We have considered two data structures
—
—
Arrays
Singly linked
 Both are linear
—
each node has one successor and one predecessor
(except the first and last)
 We now consider a hierarchical data structure
where each node may have two successors, each of
which which may have two successors, and so on
Trees in General
 A tree has a set of nodes and directed edges that
connect them
 One node is distinguished as the root
 Every node (except the root) is connected by
exactly one edge from exactly one other node
 A unique path traverses from the root to each
node
Root
Some tree terminology
Node An element in the tree references to data and other nodes
Path The nodes visited as you travel from root down
Root The node at the top It is upside down!
Parent The node directly above another node (except root)
Child The node(s) below a given node
Size The number of descendants plus one for the node itself
Leaves Nodes with no children
Height The length of a path (number of edges, -1 for empty trees)
Levels The top level is 0, increases
Degree The maximum number of children from one node
Trees used in many ways
 Hierarchical files systems
—
—
In Windows, \ represents an edge (or / in Linux)
Each directory may be empty, have children, some
of which may be other directories
• A tiny bit of MAC's file system
/
.Spotlight-V100
test
bin
sleep
etc
...
sync
...
nanorc
...
mail.rc
...
A few uses of trees
 Implement data base systems
 Store XML data from a web service as a Java
collection DOM tree
 Binary Search Trees insert, remove, and find are O(log n)
56
/ \
25 80
/ \
\
12 30 107
 Compilers: Expression tree, Symbol tree
 Store game of 20?s
 Once used as our logo
The Binary Tree
 Structure has nodes to store an element along
with the left and right children (binary trees)
—
root is like first, front, or top in a singly linked
structure
nodes
root
"T"
"L"
"R"
edges
Binary Trees
 A binary tree is a tree where all nodes have zero,
one or two children
 Each node is a leaf (no children), has a right child,
has a left child, or has both a left and right child
A
B
C
D
F
D
Application: Huffman Tree
 Binary trees were used in a famous first file
compression algorithm Huffman Tree
 Each character is stored in a leaf
 Follow the paths
—
0 go left, 1 go right
a is 01, e is 11
What is t?
—
What is
—
—
'a'
't'
0001101100100010000001000111111
—
31 bits vs. 12*8 = 96 bits 'h'
'r'
' '
'e'
Application: Binary Search Trees
 Insert, Search, Remove Operations:O(log n)
50
25
12
75
35
28
66
41
54
90
81
95
Binary Search Trees
 A Binary Search Tree (BST) data structure is a
binary tree with an ordering property
 BSTs are used to maintain order and faster
retrieval, insertion, and removal of individual
elements
 A Binary Search Tree (BST) is
—
—
an empty tree
consists of a node called the root, and two children, left
and right, each of which are themselves binary search
trees. Each BST contains a key at the root that is
greater than all keys in the left BST while also being
less than all keys in the right BST. Key fields are
unique, duplicates not allowed.
Are these BSTs?
only the keys are shown
50
Is this a BST?
25
12
75
45
66
50
Is this a BST?
25
12
90
75
55
73
90
BST Algorithms
only the keys are shown
 Think about an algorithm that retrieves a node
—
It is similar to binary search.
 Start at root, go left or right until?_____
(Ex: target == 65)
50
25
12
75
36
65
90
 Assuming the BST is "balanced", what is the tightest
upper bound in Big-O?
values must be unique
 insert
—
returns false if the key exists
In this case, the mapping is not added to the
collection
insert
only the keys are shown
 Start at the root and go either left or right to find
the insertion point.
root
tracker
50
25
12
75
36
65
90
To insert 28: 28 < 50 so go left; 28 > 25 so go right;
left link from 36 is null so stop
Adding the new node
 Replace the left child of 36, which was null, with
a new BST node with data == 28
50
25
12
75
36
28
65
90