* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download GPU Computational Geometry - University of North Carolina
Survey
Document related concepts
Transcript
By Shawn Brown - April 3rd, 2007, CS790-058
GPU COMPUTATIONAL GEOMETRY
OVERVIEW
Introduction to Computational Geometry
3 Papers in the area
COMPUTATIONAL GEOMETRY
Where am I?
Nearest neighbor search
Find all the movie theaters in a 10 mile square.
mapping
Where is the closest post office?
How do I get there?
Range queries
Geometric Problems
Think of problem & solution in geometric terms
Data structures & algorithms follow from this approach
CG APPLICATION AREAS
Computer Graphics
Robotics (motion planning)
Geographic Information Systems (mapping)
CAD/CAM (design, manufacturing)
Molecular Modeling
Pattern Recognition
Databases (queries)
AI (Path finding)
Etc…
SOME BROAD THEMES
Geometric Reasoning
Normal CS Data Structures & algorithms
Look at algorithm in reverse order to make proofs
At current step (final step), how did I get here?
Randomization techniques
Applied in geometric context
Backwards Analysis
Vertices, lines, Polygons, Half-planes, Simplexs, arrangements,
connectedness, graph theory, etc.
Randomly pick next object to work on from set
Robustness & Degeneracy's
Will algorithm work correctly under numerical accuracy
constraints
Will algorithm work correctly for co-incident, co-linear, co-planer,
redundant data, etc.
CG DATA STRUCTURES & ALGORITHMS
Convex hulls
Polygon Triangulation
Line segment intersection
Linear Programming
Minimum enclosing region (Disc, Sphere, box)
Range Searching
KD-Trees, Range Trees, Partition Trees, Simplex Trees,
Cutting trees, etc.
Point Location
Trapezoidal Maps
MORE DATA STRUCTURES & ALGORITHMS
Voronoi Diagrams
Delaunay Triangulation (dual of Voronoi)
Arrangements and Duality
Windowing (Rectangle query)
Binary Space Partitions (BSPs)
Minkowski Sums (Motion Planning)
Quad Trees
Visibility Graphs (shortest path)
GPU LIMITATIONS
Fixed size memory
Works best on stand-a-lone objects
Data Structures & algorithms need to support
Works poorly on algorithms with dependencies on previous steps
Cache coherent memory access
Coalesce memory accesses
Regular grids better than irregular meshes
Neighbor dependencies as predictable patterns
Works best on multiple objects in parallel
Each object handled has very few dependencies on neighbors
Works best on memory efficient data
Upper bound on amount of data handled
Avoid comparisons between objects and levels
Works best on algorithms with high arithmetical intensity
High cost of I/O vs. compute power
GPU SOLUTIONS
DATA STRUCTURES & ALGORITHMS
Data represented on regular grids (texture maps)
Data access patterns are regular and predictable
Data has few dependencies
Each object is independent of it’s neighbors
Any dependencies are read only, predictable, cache
coherent
Dependencies across multiple iterations are regular,
predictable, and cache coherent
Low bandwidth I/O
Lots of compute operations per I/O operation
GPU VS. CPU
Good Fits for GPU
Voronoi Diagrams, Distance Fields
Poor Fits for GPU
Binary Searches, Tree searches (KDTrees, etc.)
Can’t
parallize (next compare dependent on results of
previous compare)
Unpredictable Cache incoherent access patterns across
multiple data objects
Traditional Sorting
Bitonic
sort is exception
Reductions (from ‘n’ objects to single answer)
3 RESEARCH PAPERS
“Generic Mesh Refinement on GPU”, by Tamy
Boubekeur and Christophe Schlick, 2005
“Dynamic LOD on GPU” by Junfeng Ji, Enhua Wu, Sheng
Li, and Xuehiu Liu, 2005
“Isosurface Computation Made Simple:
Hardware Acceleration, Adaptive Refinement
and Tetrahedral Stripping” by Valerio Pascucci, Joint
Eurographics - IEEE TVCG Symposium on Visualization
(VisSym), 2004, p. 293-300.
1ST PAPER
“Generic
Mesh Refinement on GPU”
by Tamy Boubekeur and Christophe Schlick,
Proceedings of SIGGRAPH /Eurographics
Graphics Hardware, 2005, ACM Press
MESH REFINEMENT - INTRO
Geometry Mesh Refinement
Displacement
Mapping
Subdivision Surfaces
Refinement Typically done on CPU
GPU
Pipeline optimized for rendering millions of
triangles from vertex lists
But lack of support for geometry generation on GPU
Goal: How to do Mesh Refinement on GPU
DISPLACEMENT MAPPING
A texture (height map) is
used to displace
underlying geometry.
Displacement done in
direction of local surface
normal.
Re-tessellation of
original polygons into
micro-polygons
Example: Pixar’s REYES
on Renderman
*from Wikipedia.com
SUBDIVISION
The limit of an infinite refinement process
Start
with an initial polyhedral mesh, G0=(V0, E0, F0)
Subdivide via a set of rules, Gn+1 = Subdivide( Gn )
Repeat subdivision step until refined polyhedral
mesh approximates desired smooth surface.
Algorithm (One Refinement step)
New
Edge Vertices (by weighting rules)
Remesh each original face (new edges, new faces)
Perturb original vertices (by weighting rules)
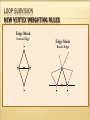
LOOP SUBVISION
NEW VERTEX WEIGHTING RULES
Edge Mask
Interior Edge
Edge Mask
1
8
3
8
Border Edge
3
8
1
8
1
2
1
2
LOOP SUBDIVISION
REMESH
Create New
Edge Vertices
Remesh
New Edges, New Faces
LOOP SUBVISION
PERTURB ORIGINAL VERTEX RULES
Vertex Mask
Vertex Mask
Ordinary Valance
1
16
1
16
n
n
1
16
5
8
1
16
Extra-ordinary Valance
1
16
1
16
n
n
n
n
n
n
1 n
n
n
n
n
n
n
2
1
2
n 40 3 2cos
64
n
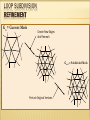
LOOP SUBDIVISION
REFINEMENT
Gn = Current Mesh
Create New Edges
And Remesh
Gn+1 = Subdivided Mesh
Perturb Original Vertices
PREVIOUS SCHEMES
Traditional subdivision schemes (Loop) require
dynamic adjacency information to implement.
Adjacency
information is cache coherent in at most
one direction (vertical or horizontal) for both reads
and writes
Works best on CPU
Works poorly on GPU
lack
of cache coherency
Hard to parrellize
GPU LIMITATIONS
Entire mesh must fit in GPU memory
LOD rendering means n copies of different size
meshes must be stored in memory
Dynamic Meshes must be updated on each
frame by CPU
Conclusion: Use/update coarse meshes on
CPU, generate refined meshes on GPU to
desired LOD.
JUSTIFICATION
Main Reason: Overcome Bandwidth Bottleneck
CPU approach:
Load coarse mesh on CPU (thousands of polygons)
Generate refined mesh on CPU (millions of polygons)
Transfer refined mesh to GPU (high bandwidth)
Render refined mesh on GPU
GPU approach:
Load coarse mesh on CPU (thousands of polygons)
transfer coarse mesh to GPU (low bandwidth)
Optionally load height map (for displacement mapping)
Optional transfer height map (for displacement mapping)
Generate refined mesh on GPU (millions of polygons)
Render refined mesh on GPU
Secondary Reason: Offload work load from CPU onto GPU
PROPOSED SOLUTION
Generic Refinement Pattern (RP - template):
Store
RP as vertex buffer on GPU
Use coarse triangle T as input to vertex shader
Update and Draw virtual triangles of RP from
attributes of input Triangle T
ALGORITHM
Render( Mesh M)
For
each coarse triangle T in M do
Place
triangle attributes TA as inputs to vertex shader
Draw parameterized RP template instead of T
MORE DETAILS
Need to map virtual vertices of pattern onto actual
attributes (<x,y,z>, <u,v>, etc.) of triangle T
Store virtual coordinates of pattern vertices V as
barycentric triple (u,v,w).
Given {P0, P1, P2} as actual positions of T
Vwuv = {w,u,v} with w = 1-u-v
Vpos = V.w * P0 + V.u * P1 + V.v * P2
Other triangle attributes (u,v, colors, etc.) can be
generated in a similar manner from virtual vertices
GPU DISPLACEMENT MAPPING
Given coarse triangle T with attributes TA
Position, texture coords, normals,etc.
<{P0,P1,P2}, {u0,u1,u2}, {v0,v1,v2}, {N0,N1,N2}>
For each vertex V in RP template
Interpolate position Pv ={x,y,z} from {P0,P1,P2}
Interpolate texture values Huv ={u,v}
Interpolate normal values Nv ={nx,ny,nz}
Use texture coords (Huv) to get value ‘h’ in height map
Compute Displaced Position
Dv
= Pv + h*Nv
PROCEDURAL DISPLACEMENT MAPPING
Texture Map access in Vertex Shader can be
slow (especially if accesses are not coherent).
Use a parameter driven function instead which
can be quickly computed in Vertex Shader
D=P+(a*sin(f*||P||)*N)
LEVEL OF DETAIL (LOD)
Store a set of larger and larger refinement
patterns on GPU = {RP0, RP1,…, RPn}
Use LOD techniques to pick appropriate LOD
pattern for refinement and rendering
LIMITATIONS TO APPROACH
No true subdivision scheme support
No geometric continuity guarantees across
shared edges of coarse triangles
LOD Scheme is not adaptive and exhibits
popping artifacts
CURVED PN TRIANGLES
Purely local interpolating
refinement scheme
Fast mesh smoothing
Provides visual smoothness
Despite lack of geometric
continuity across edges
Generate Triangle normal's
using linear or quadratic
interpolation (enhanced
triangle definition)
Offers results similar to
Modified Butterfly subdivision
scheme
PERFORMANCE
Environment:
P4 3.0 Ghz
Nvidia Quadro FX
4400 PCIe
MS Windows XP
Running on OpenGL
Conclusion: Frame rates are equivalent, #Vertices on bus greatly
reduced, CPU freed up to work on other tasks than refinement.
CONCLUSIONS
Simple Vertex Shader Method for low cost
tessellation of meshes on GPU
At cost of linear interpolation of 3 original triangle
attributes for each virtual triangle attribute in pattern
Generic and Economic PN-Triangle implementation on
GPU
Reduced bandwidth on graphics bus
Low level constant amount transferred regardless of
target refinement (use larger templates for more
refined results)
CPU freed up
to work on other tasks than refinement
2ND PAPER
Dynamic
LOD on GPU
by Junfeng Ji, Enhua Wu, Sheng Li, and Xuehui
Liu, Proceedings of Computer Graphics
International (CGI), 2005, IEEE Computer
Society Press.
INTRODUCTION
Modern Datasets are getting to large to
visualize at interactive rates
Level of Detail (LOD) methods are used to
greatly reduce the amount of geometry that
needs to be visualized
Because of complexity, LOD methods are
traditionally performed on the CPU
This paper proposes a GPU LOD technique
using shaders
PRIOR WORK
Irregular Meshes
Progressive Meshes, H. Hoppe, 1996
Hierarchical Dynamic Simplification, D. Luebke, 1997
Regular Meshes
Multi-resolution Analysis of Arbitrary Meshes, Eck et al.,
1995
Digital Elevation Models (DEMs) + LOD Quad Trees,
Lindstrom 1996 & Parojala 1998
Geometry Image Meshes, Gu & Hoppe et al., 2002
Extended to poly cube maps by Tarini et al, 2004.
Point Techniques
Qsplat, Rusinkiewicz, 2000
PROGRESSIVE MESHES
13,546
500
Mn
M175
vl
150
152
vr
M0
vl
v’s vr
vspl(vs ,vl ,vr ,vs ,vt ,…)
152
M0
M1
ecol(vs ,vt , v’ s )
vt
vs
150 faces
500
M1
M175
13,546
Mn
HIERARCHICAL DYNAMIC SIMPLIFICATION
Entire object represented as
single vertex tree
Start at base level
Collapse group of vertices
into parent representative
vertex (proxy)
Render at appropriate LOD by
traversing to level of tree
based on current viewing
parameters
GEOMETRY IMAGE MESHES
CUT
PARAMETERIZE
REGULAR GRID
RENDER
GEOMETRY IMAGE
RGB = XYZ
SAMPLE
POLY-CUBE MAPS
GIM’s have complex
distorted
parameterizations
Approximate
geometry by
polycube map
Project Geometry
onto PolyCube
Store each face of
polycube in texture
atlas
TEXTURE ATLAS
GOAL – GPU LOD GEOMETRY
Perform LOD geometry selection dynamically
on GPU
GPU limitations push us towards a regular
representation of geometry
For max efficiency, data structure must support
parallel algorithms.
PROPOSED SOLUTION
Use Geometry Image Mesh (GIM) as underlying
data structure.
Regular
structure (texture map) works very well on
GPU.
Use Polycube texture atlas for complex objects
Add LOD support via a modified Quad Tree data
structure called P-QuadTree.
OVERVIEW OF APPROACH
Creation
LOD Atlas Texture
Rendering
Select
appropriate LOD level
Render on GPU
CREATION
Generate GIM Atlas from 3D model
Generate LOD atlas from GIM
Generate additional texture maps
Normal
Map
LOD metrics
Index map (parent lookup)
CREATE GIM ATLAS
Generate Polycube from geometry object using
semi-automatic technique from Tarini et al.
Cut cube faces along edges to get individual
textures
Pack face textures into square or rectangular
texture Sample texture atlas on regular grid
Create GIM from projected samples
CREATE LOD QUADTREE ATLAS
For each chart, Texture must be (2m+1)×(2m+1)
Pad Texture with null samples
Construct QuadTree top down using GPU Kernel
Each
node represents 3x3 of vertices
Uses Restricted QuadTree triangulation
Stack all levels of LOD quadtree in LOD Atlas
Can
be done in rectangle with ratio 1:1.5
RESTRICTED QUADTREE TRIANGULATION
Avoid problems with cracks at T-intersections
Compute error at each node
Parent error always greater than children
Constrain difference in error between neighboring
vertices to never be greater than one
Check 2 nephews as well (cost of 2 texture lookups)
LOD NODES
Each node represents 3x3 vertices and 8
triangles
Easily
rendered as triangle fan
Bounding sphere around 9 vertices
Not much information in paper on how they
compute normals or normal cone…
CUTTING AND PACKING
CUTTING
PACKING
SQUARE CHARTS
CUTTING
PACKING
RECTANGULAR
CHARTS
GIM ATLAS & LOD ATLAS
4 TEXTURE MAPS REQUIRED
Geometry Map (GIM) (x,y,z) on regular grid
Center position of node
LOD Parameter map
Error (used for LOD selection)
Normal cone (used for back face culling)
bounding sphere radius (used for backface culling)
Normal Map (N.x,N.y,N.z)
Normal at center position of node
Index Map
Parent node lookup
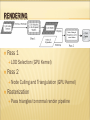
RENDERING
Pass 1
LOD
Selection (GPU Kernel)
Pass 2
Node
Culling and Triangulation (GPU Kernel)
Rasterization
Pass
triangles to normal render pipeline
LOD SELECTION (GPU KERNEL)
Parameters:
Viewing frustrum, Viewing cone
Pass in CPU LOD error threshold from viewpoint
LOD Atlas textures
Algorithm:
1. Kill invalid nodes (padded or empty pixels)
2. LOD threshold tests
Threshold test parent LOD, if passes discard current
node
Threshold test current node, keep if passes
3. Culling tests
1-1 mapping (fragments processed to texels in LOD
atlas)
Normal & Normal Cone vs. View Cone
Bounding Sphere vs. Viewing frustrum
Output:
Bitmap (true/false) of LOD fragments
CULLING & TRIANGULATION
(GPU KERNEL)
Cull node (false in LOD bitmap)
Retrieve 3x3 vertices for each valid node using vertex
texturing
Cull invalid vertices (false in LOD bitmap) by moving them to
infinity.
Keep valid vertices (true in LOD bitmap)
T-Intersection tests
Check 4 edge vertices (1,3,5,7) for possible T cracks
check 2 adjacent nephew connections for each edge
Can’t actually delete vertices from triangle fan
One position (active) = actual edge vertex position
2nd position (inactive) = move to corresponding corner vertex (disappears)
Output Triangle Fan from Vertex Shader
RENDERING PIPELINE
LOD Bitmap
LOD
Threshold
Kernel
Normal Map
Atlas
LOD QuadTree
Atlas
Rasterize
Triangles
LOD Mesh
Kernel
(Cull & Triangulate)
RESULTS
PERFORMANCE
Environment
VC++
Windows 2000
OpenGL + extensions
CPU: 2.8GHz Pentium 4
2G DRAM
NVIDIA GeforceFX 5950
256 MB of DDR RAM
texturing not available on
our GPU,
this step is estimated in
our test.
GPU approach about
10x faster than
CPU approach
LIMITATIONS
Minor discontinuity artifacts sometimes visible
No speedup in LOD algorithm itself for small
distant objects vs. full size objects O(1.5xN)
all
nodes (texels) visited in both GPU kernels
Speedup win is in rasterization (reduced #tris)
VS.
All nodes visited
Subset of nodes visited
CONCLUSIONS
Proof of this LOD technique on GPU
Robust
Efficient
(10x performance over CPU)
Dynamic LOD
Offloads work from CPU
Future work
Room
for more complex operations in shader
Adaptive Tessellation for Radiosity lighting
3RD PAPER
“Isosurface Computation Made Simple: Hardware
Acceleration, Adaptive Refinement and Tetrahedral
Stripping” by Valerio Pascucci, Joint Eurographics IEEE TVCG Symposium on Visualization (VisSym),
2004, p. 293-300.
INTRODUCTION
Use a GPU to speed up generation of Iso-Surfaces
from a 3D volume set for interactive exploration of
the data volume
Spatially subdivide 3D volume with a 3D tetrahedral
volume filling 3D curve
Find all tetra-hedrons containing desired iso-value and
interpolate a quad (or tri) approximating iso-surface in
that tetrahedron
Complete set of generated quads (tris) forms isosurface corresponding to iso-value.
Uses nested errors scheme to form consistent
meshes
ISO-CONTOURS & ISO-SURFACES
Iso-contour - All
points in a 2D data
set with the same
function value
Elevation
Maps
{x, y, z | F ( x, y, z ) C ( w)}
Iso-Surface – all
points in a 3D data
volume with the
same function value
Medical Imaging
Scientific Visualization
2D ISO-CONTOURS
SPATIAL SUBDIVISION = TRIANGULATION
Data set covered
with triangulation
2D scalar
function value
associated with
each vertex F(x,y)
Generate Isocontours for a
given Iso-Value
2D ISO-CONTOURS (INTERPOLATION)
Find triangles with
vertices that bracket
desired iso-value
C(w).
Create line segments
that approximate isocontour by
interpolating values
on triangle edges
F=0
C(w)=1.8
F=1.8
F=2
F=3
2D ISO-CONTOURS
Collection of
interpolating line
segments form
final Iso-contour
set for a given Isovalue.
3D ISO-SURFACES
Use tetrahedrons
instead of
triangles
Iso-surface
approximated by
quads (or tris)
instead of line
segments
Need to estimate
normals for quads
F=0
C(w)=2.5
F=3
F=2
F=4
PRIOR-WORK
Iso-Surfaces
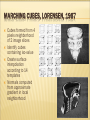
Marching Cubes, Lorenson & Cline, 1987
Octree with min/max scalars, Wilheims & Van Gelder,
1992
Span Spaces, Livnat et al, 1996, Shen et al, 1996
Occlusion Optimization, Livnat & Hansen, 1998
Multi-Pass, Gao & Shen, 2001
Nested Errors
Longest edge bisection rule, various, 1997-2001
Saturated Errors, Gerstner & Pajarola, 2000
MARCHING CUBES, LORENSEN, 1987
Cubes formed from 4
pixels neighborhood
of 2 image slices
Identify cubes
containing iso-value
Create surface
interpolation
according to 14
templates
Normals computed
from approximate
gradient in local
neighborhood
SATURATED ERRORS, GERSTNER ET AL, 2000
Extraction: Topology preserving
Iso-surface extraction from multiresolution cubes
Uses tetrahedrons to gurantee
piecewise linear connected
components
Automatically generates lookup
table of all possible valid
topologies of cube
Identifies critical points (genus
changing topology)
Simplification: reduces size of
mesh in topology preserving
manner
Sorts critical points in
importance
User defined threshold value
eliminate lower threshold critical
points from topology first
BUILDING BLOCKS
Generate quads from tetrahedrons
Compute Normals
Render quads
View Dependent Refinement
Tetrahedral Strips
3D Space Filling Curve
* Author says he uses 4 GPU Kernels to accomplish this
technique but in my opinion, he doesn’t explain it well,
so I’m not quite sure which building blocks are on GPU
and which are on CPU and how the overall flow of the
program works
QUAD GENERATION
Generate one Quad per tetrahedron
Interpolate
one vertex along each edge
Mark invalid if outside range of 2 defining vertices
3
types
Empty
tetrahedron (4 invalid = co-incident vertices)
Triangle (1 invalid = 2 co-incident vertices)
Quad (4 valid vertices)
lookup
tables for efficient interpolation &
generation
vI va 1 vb
c( w) f (vb )
f (va ) f (vb )
V0
COMPUTE NORMALS
Orientation:
(1 determinant)
x1
s sign x2
x
3
y1
Normal:
N s y2
(3 determinants)
y
3
y1
y2
y3
z1
z2
z3
where
V2
z1
z 2 where
z3
F1 z1
F2 , z2
F3 z3
F1
F2
F3
V1
V3
xi Vi .x V0 .x
yi Vi . y V0 . y
zi Vi .z V0 .z
x1 F1
x2 , F2
x3 F3
x1
x2
x3
Fi F (Vi ) F (V0 )
Note: F can be stored in vertex.w coordinate for efficiency
y1
y2
y3
T
QUAD RENDERING
Draw quads in OpenGL directly
Rely
on OpenGL to solve problems
Throw
away invalid quads (4 co-incident vertices)
Reduce quad to triangle (2 co-incident vertices)
Use computed normals for shading
VIEW DEPENDENT
REFINEMENT
Adaptively refine a tetrahedral mesh
Bi-sect the longest edge of tetrahedron creating
2 new tetrahedrons
Similar to Octree
Given a cube divided into 6 tetrahedrons
3 sub-divisions of tetrahedrons gives you a new
smaller grid of 8 cubes (1 level of octree subdivision)
Cube subdivision can be done via a simple rule
pattern without ever measuring lengths
VIEW DEPENDENT REFINEMENT, CONT
VIEW DEPENDENT
REFINEMENT, III
Each split point is actually at center of several tetrahedrons
which form a shape called a diamond.
Each tetrahedron can be associated with the vertex that
caused it’s split into a diamond shape
The hierarchy of refined tetrahedrals forms a binary tree
The hierarchy of diamonds is more complicated and takes the
form of a directed acyclic graph (DAG).
Starting from a uniform grid guarantees a predictable
pattern to the size and shape of tetrahedrons
IE no need to store auxillary info, it can be calculated based on
the level of the subdivision)
VIEW DEPENDENT REFINEMENT - ALGORITHM
Refine Mesh( tetra, level, tier )
v = Bisect longest edge, by tier pattern (0,1,2)
If (level == max level) or satisfies_tolerance( v, level )
Draw_ISO_Surface( tetra )
Cull Mesh
Bisection point outside min, max bounding distances
Bounding sphere of diamond outside view frustrum
Recursively refine mesh, by tier pattern (0,1,2)
RefineMesh(
left tetra, level + 1, (tier++) % 3))
RefineMesh( right tetra, level+1, (tier++) % 3 )
SATISFIES_TOLERANCE( V, LEVEL )
projects the error of vertex v onto the current view
plane from the closest point of bounding sphere of
diamond
View plane can be computed from level
Size of bounding sphere can also be computed from
level
Returns true if projected error is smaller than a
given threshold tolerance (global variable)
Written to guarantee that if any diamond is
included in the current mesh then all it’s parents
are also included.
Therefore the adaptive mesh will have no cracks
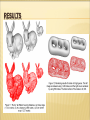
RESULTS OF ADAPTIVE REFINEMENT
Adaptive
Non-Adaptive
TETRAHEDRAL STRIPS (STREAMING)
Transferring all the vertices of base level
tetrahedrons from CPU to GPU consumes a lot of
bandwidth
Use tetrahedral strips similar to triangular strips in
2D to reduce vertex bandwidth
Any 2 adjacent tetrahedrons have 3 vertices in common
(meaning only 1 new vertex needs to be transferred).
Use adjacency graph info to build strips
Results in a 60% decrease in vertex bandwidth
3D SPACE FILLING CURVE
The Author
recommends using a
new 3D space filling
based on sierpinksi’s
curve adapted for
tetrahedrons that fills
1/6 of a cube. 6 such
curves fill a 3D cube.
Author provides no
details other than
some pictures and a
link to another paper
PERFORMANCE RESULTS
*800 Mhz Pentium CPU
800 RAM Main Memory
Linux Operating System
CONTRIBUTIONS
Simple technique for generating Iso-Surfaces presented
from a 3D volume data set
Adaptive Refinement
based on viewing direction
Uses longest edge bi-section
Uses nested errors scheme to avoid cracks in meshes
Tetrahedral Strips
Using tetrahedrons + OpenGL quads
Allows interactive rendering of 512x512x512 data sets
Optimizes bandwidth from CPU to GPU
3D space filling curve