Download TOPIC 3: Linear Equations and Inequalities  2 4

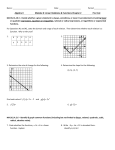
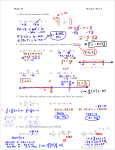
TOPIC 3: Linear Equations and Inequalities
1. Solve:
2x  4
2
 .
x6
15
2. Solve for the common solutions by substitution or linear combinations. State whether the
lines are parallel, perpendicular, intersecting but not perpendicular, or the same line.
x  y  5

2 x  y  1
3. Solve for the common solutions by substitution or linear combinations. State whether the
lines are parallel, perpendicular, intersecting but not perpendicular, or the same line.
2 x  y  3

4 x  6  2 y
4. Find the slope and the y-intercept. Then sketch the graph: 3x  2 y  6 .
5. Find an equation of the line through (– 3, – 5) and (2, – 2).
6. Graph and write an equation for the vertical line through the point (– 2, 3).
7. Solve and graph on the number line:  2 x  3  9 .
8. Solve the inequality: 2 x  3 y  12 , and shade the
solutions on the graph provided.
9. Solve and graph on the number line: 3  5 x  2 .
10. Solve and graph on the number line: 1  2 x  7 .
1
ANSWERS TOPIC 3: Linear Equations and Inequalities
1. x 
7. x  3
3
2
2. (– 6, – 11); The lines are intersecting but
not perpendicular.
3. When you solve this system, you will
get an equation that is true always, such
as 0 = 0 or something similar. The lines
are the same line, and any solution to the
line will be a solution to the system.
Writing x, y  | 2 x  y  3 or
x, y  | 4 x  6  2 y are equivalent ways
to write all solutions.
4.
Slope is
8.
3
; y-intercept = (0,– 3)
2
9.
x
1
or x  1
5
0
1
5
2
5
3
5
4
5
1
10. x  3 or x  4
5. y 
6.
3
3
16
or  y  2    x  2
x
5
5
5
x  2
For more examples, click here
2