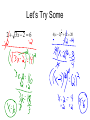* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Algebra 2 Lesson 7
Two-body problem in general relativity wikipedia , lookup
Schrödinger equation wikipedia , lookup
BKL singularity wikipedia , lookup
Maxwell's equations wikipedia , lookup
Calculus of variations wikipedia , lookup
Euler equations (fluid dynamics) wikipedia , lookup
Equation of state wikipedia , lookup
Navier–Stokes equations wikipedia , lookup
Derivation of the Navier–Stokes equations wikipedia , lookup
Equations of motion wikipedia , lookup
Schwarzschild geodesics wikipedia , lookup
Computational electromagnetics wikipedia , lookup
Differential equation wikipedia , lookup
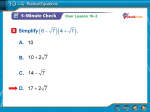
7.5 Solving Radical Equations What is a Radical Equation? • A Radical Equation is an equation that has a variable in a radicand or has a variable with a rational exponent. 3 x 10 2 3 yes ( x 2) 25 yes 3 x 10 no EXAMPLE – Solving a Radical Equation 5x 1 6 0 5x 1 6 2 2 5 x 1 ( 6 ) 5x 1 36 5x 35 x7 Square both sides to get rid of the square root Let’s Try Some 2 3x 2 6 1 2 4( x 2) 12 20 RADICAL EQUATIONS 3(5n 1) 2 0 1 3 3(5n 1) 2 1 (5n 1) 3 2 3 1 3 3 (5n 1) 3 2 3 (5n 1) 8 27 1 3 5n 8 27 1 5n 8 27 27 27 5n 35 27 ISOLATE RADICAL / RATIONAL RAISE BOTH SIDES TO RECIPROCAL POWER SOLVE FOR THE VARIABLE n 7 27 RADICAL EQUATIONS 2(n 2) 3 50 2 2(n 2) 3 50 2 2 2 ISOLATE RADICAL / RATIONAL RAISE BOTH SIDES TO RECIPROCAL POWER (n 2) 25 2 (n 2) 2 3 3 32 25 3 2 n 2 125 n 2 125 n 127 or n 123 Use absolute value when taking an even number root. Checking for extraneous solutions x 3 5 x x 3 x 5 ( x 3 ) 2 ( x 5) 2 x 3 x 2 10 x 25 0 x 2 11x 28 0 ( x 4)( x 7) x 4 or x 7 So check answers with x 4 or x 7 SOLVING MORE COMPLEX EQUATIONS (2 x 1) 0.5 (3x 4) (2 x 1) 0.5 0.25 0 (3x 4) 1 2 4 0.25 1 4 4 [(2 x 1) ] [(3x 4) ] 2 (2 x 1) 3x 4 Raise each side to the 4th power. This will get you integer powers – much easier to work with! 4 x 2 4 x 1 3x 4 4x2 x 3 0 3 x ,1 4 Factor check for extraneous solutions (2 x 1) 0.5 (3x 4) 0.25 0 3 x ,1 4