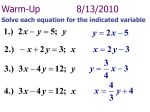Download 3-2 Solving Systems Algebraically (p. 125)

3-2 Solving Systems
Algebraically (p. 125)
Algebra 2
Prentice Hall, 2007
Content Objectives
You will…
Solve a system of linear equations
using the process of SUBSTITUTION.
Solve a system of linear equations
using the process of ELIMINATION.
Be able to decide which method would
be the easiest to use.
Substitution Method
1. Choose 1 equation and solve for the
“easiest” variable.
2. Substitute that “expression” into the other
equation for the variable it represents.
3. Solve for the 2nd variable.
4. Substitute the value of that variable into 1 of
the 2 original equations to find the value of
the 1st variable.
Example
Solve the system using substitution:
3x  y  0
4x  3y  26

Hint: Solve for y in the 1st equation.
Example
Solve the system using substitution:
x  2y  1
x  4y  6

Hint: Solve for x in either equation.
Elimination Method
1. Write both equations in Standard Form.
2. “Doctor-up” 1 or both equations so that the
x’s OR y’s are zero pairs.
3. Combine the 2 equations, thereby
eliminating one of the variables.
4. Solve for the remaining variable.
5. Substitute the value of that variable into
either of the original equations to find the
other variable.
Example
Solve the system using elimination:
x  2y  1
x  4y  6

Hint: Doctor-up one equation in order to
eliminate x.
Example
Solve the system using elimination:
3x  7y 15
5x  2y  4

Hint: Doctor-up both equations in order
to eliminate x OR y... Your choice!

Example
Solve the system using whichever
method you want:
2x  4y  6
3x  6y  8
No Solution!
What if…?
… both variables get eliminated and you
end up with a false statement?
NO Solution
… both variables get eliminated and you
end up with a true statement?
Infinite # of Solutions
Homework
3-2 p. 128: m.o.5 (5-50)