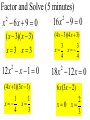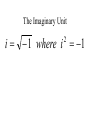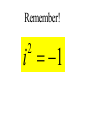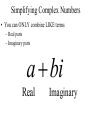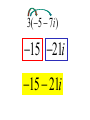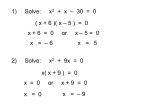* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Radicals and Radical Expressions
Survey
Document related concepts
Transcript
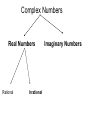
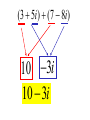
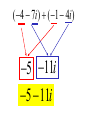
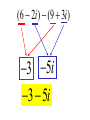
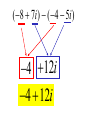
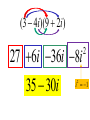
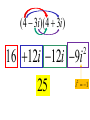
Factor and Solve (5 minutes) 2 2 16 x 9 0 x 6x 9 0 ( x 3)( x 3) x3 x3 12 x x 1 0 2 (4 x 3)(4 x 3) 3 3 x x 4 4 18 x 12 x 0 2 (4 x 1)(3 x 1) 6 x(3 x 2) 1 x 4 2 x0 x 3 1 x 3 Simplifying Radicals and Complex Numbers Objectives • I can simplify Radicals to Lowest Terms • I can simplify negative radicals using “i” • I can simplify complex numbers using – Addition – Subtraction – Multiplication Symbols • Radical symbol Radical Index# Radicand Radical Basics • If there is no index number listed, it is assumed to be a 2 (Square Root) • The index number determines what root we are looking for Method for Simplifying • Prime Factor the number under the house (radical) • Look at the value of the index number • Cross off the index number of numbers or variables to bring one out of the house. • If you don’t have enough, then they stay under the house. Example 1 • Simplify: 36 2 2 33 2 2 33 23 6 • Factor the 36 36 2 18 2 9 3 3 Example 2 • Simplify: 12 • Factor the 12 12 2 23 2 23 2 3 2 6 2 3 Example 3 32 4 2 Example 3 20 2 5 Complex Numbers Real Numbers Rational Irrational Imaginary Numbers Complex Numbers The set of all numbers that can be written in the format: a + bi ; “a” is the real number part “bi’ is the imaginary part The Imaginary Unit i 1 where i 1 2 Example 4 20 2 5i Example 5 9 3i Example 6 48 4 3i Remember! i 1 2 Simplifying Complex Numbers • You can ONLY combine LIKE terms – Real parts – Imaginary parts a bi Real Imaginary (3 5i ) (7 8i) 10 3i 10 3i (4 7i) (1 4i) 5 11i 5 11i (6 2i) (9 3i) 3 5i 3 5i (8 7i ) (4 5i ) 4 12i 4 12i 3(5 7i ) 15 21i 15 21i 4(9 6i ) 36 24i 36 24i (3 4i )(9 2i) 27 6i 36i 8i 35 30i 2 i 1 2 (4 3i)(4 3i) 16 12i 12i 9i 25 2 i 1 2 Homework • WS 5-2 • Quiz next class