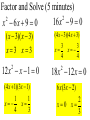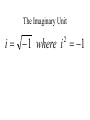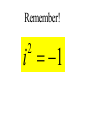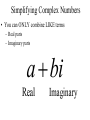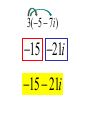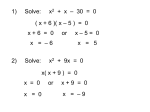Download Radicals and Radical Expressions

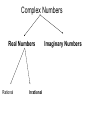
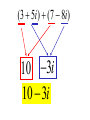
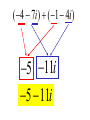
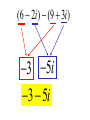
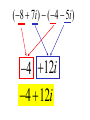
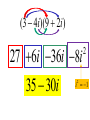
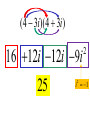
Factor and Solve (5 minutes)
2
2
16 x  9  0
x  6x  9  0
( x  3)( x  3)
x3 x3
12 x  x  1  0
2
(4 x  3)(4 x  3)
3
3
x
x
4
4
18 x  12 x  0
2
(4 x  1)(3 x  1)
6 x(3 x  2)
1
x
4
2
x0 x
3
1
x
3
Simplifying Radicals and
Complex Numbers
Objectives
• I can simplify Radicals to Lowest Terms
• I can simplify negative radicals using “i”
• I can simplify complex numbers using
– Addition
– Subtraction
– Multiplication
Symbols
• Radical symbol
Radical
Index#
Radicand
Radical Basics
• If there is no index number listed, it is
assumed to be a 2 (Square Root)
• The index number determines what root we
are looking for
Method for Simplifying
• Prime Factor the number under the house
(radical)
• Look at the value of the index number
• Cross off the index number of numbers or
variables to bring one out of the house.
• If you don’t have enough, then they stay
under the house.
Example 1
• Simplify:
36
2  2 33
2  2 33
23
6
• Factor the 36
36
2 18
2 9
3 3
Example 2
• Simplify:
12
• Factor the 12
12
2 23
2 23
2 3
2
6
2
3
Example 3
32
4 2
Example 3
20
2 5
Complex Numbers
Real Numbers
Rational
Irrational
Imaginary Numbers
Complex Numbers
The set of all numbers that can be written
in the format: a + bi ;
“a” is the real number part
“bi’ is the imaginary part
The Imaginary Unit
i   1 where i  1
2
Example 4
20
2 5i
Example 5
9
3i
Example 6
48
4 3i
Remember!
i  1
2
Simplifying Complex Numbers
• You can ONLY combine LIKE terms
– Real parts
– Imaginary parts
a  bi
Real
Imaginary
(3  5i )  (7  8i)
10 3i
10  3i
(4  7i)  (1  4i)
5 11i
5  11i
(6  2i)  (9  3i)
3 5i
3  5i
(8  7i )  (4  5i )
4 12i
4  12i
3(5  7i )
15 21i
15  21i
4(9  6i )
36 24i
36  24i
(3  4i )(9  2i)
27 6i 36i 8i
35  30i
2
i  1
2
(4  3i)(4  3i)
16 12i 12i 9i
25
2
i  1
2
Homework
• WS 5-2
• Quiz next class