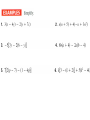Download Objective

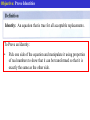
Honors Algebra 2
Chapter 1
Real Numbers, Algebra, and Problem Solving
1.1 Real Numbers and Operations
There is exactly one real number for each point on a number line.
Objective: Show that a number is rational and distinguish between
rational and irrational numbers.
If a real number cannot be expressed as a ratio of 2 integers
then it is called irrational.
Absolute Value of a Number
• The absolute value of a number is the distance
on a number line the number is from 0.

Distance from 0 is 2
|-2| = 2
Objective: Add positive and negative numbers.
Objective: Subtract positive and negative numbers.
The additive inverse of a number is the number added to it to get 0.
Objective: Add positive and negative numbers.
Objective: Subtract positive and negative numbers.
Objective: Divide positive and negative numbers.
The reciprocal/Multiplicative Inverse of a number is the number we
multiply it by to get 1.
Objective: Divide positive and negative numbers.
Objective: Recognize division by zero as impossible
Thus we cannot define and must exclude division by 0.
Zero is the only real number that does not have a reciprocal.
Is it sometimes, always, or never true that, if x is a real
number, (- x)( - x) is negative?
Is it sometimes, always, or never true that, if x is a real
number, (x)( - x) is negative?
Is it sometimes, always, or never true that, if x is a real
number, (x)(x) is negative?
1.3 Algebraic Expressions and
Properties of Real Numbers
Variable: Any symbol that is used to represent various numbers
Constant: Any symbol used to represent a fixed number
Objective: Use number properties to write equivalent expressions.
Equivalent Expressions: Expressions that have the same value for
all acceptable replacements.
Objective: Use number properties to write equivalent expressions.
Objective: Use number properties to write equivalent expressions.
Additive Identity: The number 0.
Multiplicative Identity: The number 1
For Exercises 1-4, use the properties of real numbers
to answer each question.
1. If m + n = m, what is the value of n?
2. If m - n = 0, what is the value of n? What is n called
with respect to m?
3. If mn = 1, what is the value of n? What is n called
with respect to m?
4. If mn = m, what is the value of n?
Suppose we define a new operation @ on the set of real numbers as
follows: a @ b = 4a - b. Thus 9 @ 2 = 4(9) - 2 = 34. Is @ commutative?
That is, does a @ b = b @ a for all real numbers a and b?
1.4 The Distributive Property
Objective: Use the distributive property to multiply.
Objective: Use the distributive property to factor expressions.
Factoring: The reverse of multiplying.
To factor an Expression: To find an equivalent expression that
is a product.
Objective: Collect like terms.
Like Terms: Terms whose variables are the same
Objective: Write the inverse of a sum.
1.5 Solving Equations
Objective: Solve equations using the addition and multiplication
properties.
A mathematical sentence A = B says that the symbols A and B
are equivalent.
Such a sentence is an equation.
The set of all acceptable replacements is the replacement
set.
The set of all solutions is the solution set.
Objective: Solve equations using the addition and multiplication
properties.
Objective: Prove Identities
Identity: An equation that is true for all acceptable replacements.
To Prove an Identity:
•
Pick one side of the equation and manipulate it using properties
of real numbers to show that it can be transformed so that it is
exactly the same as the other side.
HW #1.1-5
Pg 8 35-38
Pg 13 53-57
Pg 19 52-53
Pg 25 77-80
Pg 29 54-56
HW Quiz #1.1-5
Wednesday, May 24, 2017
Pg 8 38
Pg 13 56
Pg 25 78
Pg 29 56
Pg 8 36
Pg 13 54
Pg 2580
Pg 29 54
Row 1, 3, 5
Row 2, 4, 6
1.6 Writing Equations
Objective: Become familiar with and solve simple algebraic problems
At 6:00 AM the Wong family left for a vacation trip and
drove south at an average speed of 40 mph. Their friends, the
Heisers, left two hours later and traveled the same route at an
average speed of 55 mph. At what time could the Heisers
expect to overtake the Wongs?
Objective: Become familiar with and solve simple algebraic problems
It has been found that the world record for the men's
10,000-meter run has been decreasing steadily since 1950.The
record is approximately 28.87 minutes minus 0.05 times the
number of years since 1950. Assume the record continues to
decrease in this way. Predict what it will be in 2010.
Objective: Become familiar with and solve simple algebraic problems
An insecticide originally contained ½ ounce of pyrethrins. The
5
new formula contains oz of pyrethrins. What percent of the
8
pyrethrins of the original formula does the new formula
contain?
1.7 Exponential Notation
Objective: Simplify expressions with integer exponents.
Objective: Simplify expressions with integer exponents.
Thus we can say that bn and b-n are reciprocals
1.8 Properties of Exponents
Objective: Multiply or divide with exponents.
Objective: Multiply or divide with exponents.
We do not define 0°. Notice the following.
00  011
 01  01
01 0
 1   Undefined
0 0
Objective: Use exponential notation in raising powers to powers.
Objective: Use exponential notation in raising powers to powers.
Objective: Use the rules for order of operations to simplify expressions.
1.10 Field Axioms
Objective: Use the definition of a field
Field: Any number system with two operations defined in which all
of the axioms of real numbers hold
The set of Real numbers forms a field with Addition and Multiplication
Objective: Use the definition of a field
Objective: Use the definition of a field
Objective: Write Column Proofs
Objective: Write Column Proofs
Objective: Write Column Proofs
HW #1.6-10
Pg 34 23-24
Pg 37 37-41
Pg 43 58-65
Pg 52-53 12-25
The End Chapter 1