Download Systems of Linear Equations (1997

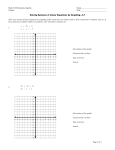
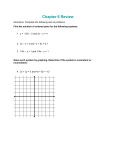
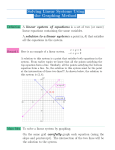
Chapter 8

A relationship between
an independent and a
dependent variable in
which as the
independent variable
changes the
dependent variable
changes by a constant
amount.
Examples:
Profit made based on
the number of tickets
sold to a dance
 Constant population
growth over time
 Cost for an appliance
repair based on a set
fee and an hourly price





Two relations that represent a comparison
with the same information
A set of equations with the same variables
Two lines in the same coordinate plane
Text p. 454
World Records
Let s = swim time
f = float time
 Which is independent?



An equation to
represent the record
holders time:
f + 3s = 44
 An equation to
represent the amount
of time available to
swim and float:
f + s = 24


f + 3s = 44

S + f = 24





Graphs
Equations
Mappings
Ordered Pairs
Tables


Lines in a plane can :
be Parallel…Never intersect
 These lines will have no solution

Intersect at only one point
 These lines will yield one solution

be Co-linear…the same line (one line a scale
factor of the other)
 These lines will have an infinite number of
solutions
1.) x + 2y = 1
2x + 5 = y
2.) 3x – y = 2
12x – 4y = 8
3.) x – 2y = 4
x = 2y - 2

Intersect or are co-linear are said to be
consistent because there is at least one
ordered pair (point) common to both lines.
 Co-linear have an infinite number of common
points!

Are parallel are said to be inconsistent
because there is not one point common to
both lines



If a system has exactly one solution, it is
independent, so…. Intersecting lines are
independent!!!
If a system has an infinite number of solutions
then it is dependent ……Co-linear lines are
dependent!!!
These terms DO NOT apply to Parallel Lines
1.) y = 3x – 4
y = -3x + 4
3.) y = -6
4x + y = 2
2.) x + 2y = 5
2x + 4y = 2
4.) 2x + 3y = 4
-4x – 6y = -8
* Check with graphing
calculator
The solution when graphing may not be exact
Example: p. 262 Census problem


Substitution
Elimination
 Addition and Subtraction
 Multiplication and Division





Solve for one of the variables in one of the
two equations
Which one??
The one with a coefficient of 1 or with the
easiest coefficient to solve for
Substitute the expression equal to the
variable into the other equation and solve for
the other variable
Use this value to find the value for the
original variable.
1.) x + 4y = 1
2x – 3y = -9
2.) 5/2x + y = 4
5x + 2y = 8
3.) 3x + 4y = 7
3/2x + 2y = 11
EJH Labs needs to make
1000 gallons of a 34%
acid solution. The only
solutions available are
25% acid and 50% acid.
How many gallons of
each solution should
be mixed to make the
34% solution?
A metal alloy is 25%
copper. Another metal
alloy is 50% copper.
How much of each
alloy should be used to
make 1000 grams of
metal alloy that is 45%
copper?
Addition and
Subtraction
 Use this method when
one of the variables’
coefficients in the two
equations is the same
or are additive inverses
 Add or subtract the
equations to eliminate
a variable

Examples:
1.) ex p. 469
2a + 4c = 30
2a + 2c = 21.5

2.) 3x – 2y = 4
4x + 2y = 4
The sum of two numbers
is 18. The sum of the
greater number and
twice the smaller
number is 25. Find the
numbers.

The sum of two
numbers Is 27. Their
difference is 5. Find
the numbers.

Lena is preparing to take the SATs. She has
been taking practice tests for a year and her
scores are steadily improving. She always
scores about 150 higher on math than she
does on verbal. She needs a 1270 to get into
the college she has chosen. If she assumes
that she will still have that 150 difference
between the two tests, what will she have to
score on each part?
Multiplication and
Division (Scaling)
 Use this method when
all variables have
different coefficients


Example p. 475


75p + 30n = 40.05
50p + 60n = 35.10
1.) 2x + 3y = 5
5x + 4y = 16
2.) 3x + 5y = 11
2x + 3y = 7
3.) 2x – 3y = 8
-5x + 2y = 13


A bank teller reversed the digits in the
amount of a check and overpaid the
customer by $9. The sum of the digits in the
two digit amount was 9 Find the amount of
the check.
Example 2 and 3 p. 477

Graphing?

Substitution?

Elimination?