* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Fast Fourier Transform
Fourier transform wikipedia , lookup
Corecursion wikipedia , lookup
Computational electromagnetics wikipedia , lookup
Eigenvalues and eigenvectors wikipedia , lookup
Inverse problem wikipedia , lookup
Discrete cosine transform wikipedia , lookup
Discrete Fourier transform wikipedia , lookup
Factorization of polynomials over finite fields wikipedia , lookup
Fast Fourier
Transform
Irina Bobkova
Overview
I. Polynomials
II. The DFT and FFT
III. Efficient implementations
IV. Some problems
Representation of polynomials
A polynomial in the variable x over an algebraic field F is
representation of a function A(x) as a formal sum
n 1
A( x) a j x j
j 0
•Coefficient representation
a (a0 , a1 ,...an1 )
•Point-value representation
{( x0 , y0 ),( x1, y1 ),...,( xn1, yn1 )}
Coefficient
representation
Point-value representation
Adding
( n)
( n)
Multiplication
( n 2 )
( n)
Interpolation
Interpolation-the inverse of evaluation –determining the
coefficient form from a point-value representation
Lagrange’s formula
n 1
( x x j )
A( x) yk jk( x x )
k j
k 0
j k
The coefficients can be computed in time (n2 )
Exercise. Prove it.
Thus, n-point evaluation and interpolation are well-defined inverse
operations between two representations. The algorithms
described above for these problems take time (n2 ) .
Fast multiplication
Question.Can we use the linear-time multiplication method for
polynomials in point-value form to expedite polynomial
multiplication in coefficient form?
Answer.Yes, but we are to be able to convert quickly from one form to
another.
a 0 , a1 ,...., a n 1
b0 , b1 ,...., b n 1
Ordinary multiplication
Time Θ(n²)
Evaluation
Time Θ(n lg n)
Interpolation
Time Θ(n lg n)
A(02n ), B(02n )
A(12n ), B(12n )
1
2n 1
A(2n
2n ), B( 2n )
c0 , c1 ,..., c2n 2
C(02n )
Pointwise multiplication
Time Θ(n)
C(12n )
1
C(2n
2n )
Complex roots of unity
Zn 1 0
There are exactly n complex roots of unity.They form a cyclic
multiplication group:
k e
2 i
2 ik
n
The value 1 e n is called the primitive root of unity; all of the
other complex roots are powers of it.
Discrete Fourier Transform
n 1
n2
Let F(x) be the polynomial F ( x) an1 x a n2 x ... a0 with degreebound n, which is a power of 2. is a primitive n-th root of unity.
yk F ( k ) .Then
Let
y0 1
1
y
1
y2 1
y 1
n 1
1
1
2
4
n 1
2( n 1)
2
a0
a1
2( n 1) * a2
( n 1) 2
an 1
1
n 1
The vector y ( y0 , y1,... yn1 )
is called the Discrete Fourier Transform of
vector a. The matrix is denoted by
Fn (. )
How to find Fn-1?
Proposition. Let be a primitive l-th root of unity over a field L.Then
0 if l > 1
k
k 0
1 otherwise
l 1
Proof. The l =1 case is immediate since =1.
Since is a primitive l-th root, each k ,k0 is a distinct l-th root of unity.
Z l 1 ( Z l0 )( Z l )( Z l2 )...(Z ll 1 )
l 1
Z ( ) Z
l
k 0
k
l
l 1
l 1
... (1) lk
l
k 0
Comparing the coefficients of Zl-1 on the left and right hand sides of this
equation proves the proposition.
Inverse matrix to Fn
Proposition. Let ω be an n-th root of unity.Then,
Fn () Fn (1 ) nE n
Proof.
The ijth element of Fn ()Fn (1 ) is
n-1
ik
ik
k=0
n-1
k=0
k(i j)
0, if i j
n, otherwise
The i=j case is obvious.If ij then i j will be a primitive root of unity of
order l, where l|n.Applying the previous proposition completes the proof.
So,
Fn1 ()
1
Fn (1 )
n
Evaluating
y= Fn () a
Interpolation
1
1
a= Fn ( ) y
n
Fast Fourier Transform
A[0] (x) a 0 a 2 x a 4 x 2 ... a n 2 x n / 21
A[1] (x) a1 a 3 x a 5 x 2 ... a n 1x n / 21
A(x) A[0] (x 2 ) xA[1] (x 2 )
So, the problem of evaluating A(x) reduces to:
1. Evaluating the degree-bound n/2 polynomials
A[0] (x) and A[1] (x)
2. Combining the results
Recursive FFT
1
2
3
n length[a]
if n=1
then return a
4
n e
5
1
6
a [0] (a 0 ,a 2 ,...,a n-2 )
7
a [1] (a1 ,a 3 ,...,a n-1 )
8
y[0] Recursive-FFT(a [0] )
2 i
n
9 y[1] Recursive-FFT(a [1] )
10 for k 0 to n/2-1
11
do y k y[0]
+y[1]
k
k
12
[1]
y k+(n/2) y[0]
k -y k
13
n
14 return y
Time of the Recursive-FFT
To determine the running time of procedure Recursive-FFT, we note, that
exclusive of the recursive calls, each invocation takes time Θ(n), where n is
the length of the input vector.The recurrence for the running time is therefore
T(n) = 2T(n/2) + Θ(n) = Θ(n log n)
More effective implementations
k [1]
The for loop involves computing the value n yk twice.We can change the
loop(the butterfly operation):
for k 0 to n/2-1
do t yk[1]
yk yk[0] +t
yk+(n/2) yk[0] -t
n
yk[0]
yk[0]
yk[0] nk yk[1]
yk[0] nk yk[1]
kn
.
Iterative FFT
(a0 , a1 , a2 , a3 , a4 , a5 , a6 , a7 )
(a1 , a3 , a5 , a7 )
(a0 , a2 , a4 , a6 )
(a0 , a4 )
(a0 )
1)
(a1 , a5 )
(a2 , a6 )
( a4 )
( a2 )
(a6 )
(a1 )
(a3 , a7 )
(a5 )
(a3 )
(a7 )
We take the elements in pairs, compute the DFT of each pair, using one
butterfly operation, and replace the pair with its DFT
2) We take these n/2 DFT’s in pairs and compute the DFT of the four vector
elements
.
.
log 2 n) We take 2 (n/2)-element DFT’s and combine them using n/2 butterfly
operations into the final n-element DFT
Iterative-FFT.Code.
0,4,2,6,1,5,3,7000,100,010,110,001,101,011,111000,001,010,011,100,101,110,111
BIT-REVERSE-COPY(a,A)
nlength [a]
for k0 to n-1
do A[rev(k)]ak
ITERATIVE-FFT
1.
BIT-REVERSE-COPY(a,A)
2.
nlength [a]
3.
for s1 to log n
4.
do m2s
5.
m e2i/m
6.
for j0 to n-1 by m 1
7.
for j0 to m/2-1
8.
do for kj to n-1 by m
9.
do t A[k+m/2]
10.
uA[k]
11.
A[k]u+t
12.
13.
14.
A[k+m/2]u-t
m
return A
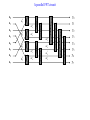
A parallel FFT circuit
a0
a1
a2
a3
a4
a5
a6
a7
0
2
04
02
14
80
02
02
18
04
82
14
83
y0
y1
y2
y3
y4
y5
y6
y7
Problem: evaluating all derivatives of a polynomial at a point
a.
Given coefficients b0,b1,…, bn-1 such that
n 1
A( x) b j ( x x0 ) j
j 0
b.
Show how to compute A(t) (x0), for t=0,1,2,…,n-1, in O(n) time.
k
Explain how to find b0,b1,…, bn-1 in O(n lg n) time, given A( x0 n ) for
k=0,1,2,…,n-1.
Problem: Toeplitz matrices
A Toeplitz matrix is an n × n matrix A ( aij ) , such that aij ai 1, j 1
for i=2,3,…,n and j=2,3,…,n.
a.
Is the sum of two Toeplitz matrices necessarily Toeplitz? What about the
product?
b.
Describe how to represent a Toeplitz matrix so that two n × n Toeplitz
matrices can be added in O(n) time.
c.
Give an O(n lg n)-time algorithm for multiplying an n × n Toeplitz matrix by
a vector of length n. Use your representation from part (b).
d.
Give an efficient algorithm for multiplying two n × n Toeplitz matrices.
Analyze its running time.