Chapter 11 Fourier Analysis
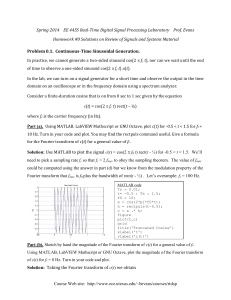
... Example 1 Figure 277 shows the input (multiplied by 0.1) and the output. For n=5 the quantity Dn is very small, the denominator of C5 is small, and C5 is so large that y5 is the dominating term in (7). Hence the output is almost a harmonic oscillation of five times the frequency of the driving forc ...
... Example 1 Figure 277 shows the input (multiplied by 0.1) and the output. For n=5 the quantity Dn is very small, the denominator of C5 is small, and C5 is so large that y5 is the dominating term in (7). Hence the output is almost a harmonic oscillation of five times the frequency of the driving forc ...
n-dimensional Fourier Transform
... high spatial frequencies. The spectrum The Fourier transform of a function f (x1 , x2 ) finds the spatial frequencies (ξ1 , ξ2 ). The set of all spatial frequencies is called the spectrum, just as before. The inverse transform recovers the function from its spectrum, adding together the correspondin ...
... high spatial frequencies. The spectrum The Fourier transform of a function f (x1 , x2 ) finds the spatial frequencies (ξ1 , ξ2 ). The set of all spatial frequencies is called the spectrum, just as before. The inverse transform recovers the function from its spectrum, adding together the correspondin ...
Lecture3.pdf
... phenomenon. The cure is to use non-equispaced nodes, for example Chebyshev nodes. • Fourier interpolation is useful for periodic functions. On a discrete grid, Fourier interpolation is prone to aliasing error. However, if the grid is fine enough, the sampling theorem ensures that Fourier interpolati ...
... phenomenon. The cure is to use non-equispaced nodes, for example Chebyshev nodes. • Fourier interpolation is useful for periodic functions. On a discrete grid, Fourier interpolation is prone to aliasing error. However, if the grid is fine enough, the sampling theorem ensures that Fourier interpolati ...
Document
... The closest pair problem Given a set S of n points, find a pair of points which are closest together. 1-D version: solved by sorting time: O(n log n) 2-D version: ...
... The closest pair problem Given a set S of n points, find a pair of points which are closest together. 1-D version: solved by sorting time: O(n log n) 2-D version: ...
Solutions
... The process of extracting the baseband signal from a bandpass signal is known as downconversion. ...
... The process of extracting the baseband signal from a bandpass signal is known as downconversion. ...
ppt
... The FFT produces approximate results. There are always artifacts introduced throughout the process ●These artifacts manifest as noise within the spectrum ●Filter out the noise using thresholds The FFT does not deal well with discontinuities ●Discontinuities manifest (typically) as high frequency noi ...
... The FFT produces approximate results. There are always artifacts introduced throughout the process ●These artifacts manifest as noise within the spectrum ●Filter out the noise using thresholds The FFT does not deal well with discontinuities ●Discontinuities manifest (typically) as high frequency noi ...
Document
... The continuous time Laplace transform is important for two reasons: • It can be considered as a Fourier transform when the signals had infinite energy • It decomposes a signal x(t) in terms of its basis functions est, which are only altered by magnitude/phase when passed through a LTI system. ...
... The continuous time Laplace transform is important for two reasons: • It can be considered as a Fourier transform when the signals had infinite energy • It decomposes a signal x(t) in terms of its basis functions est, which are only altered by magnitude/phase when passed through a LTI system. ...
Applications in Astronomy
... Linear programming algorithms solve problems in this form: maximize cT x subject to Ax = b, x ≥ 0, where b and c are given vectors and A is a given matrix. Of course, x is a vector. ampl converts a problem from its “natural” formulation to this paradigm and then hands it off to a solver. IMPORTANT: ...
... Linear programming algorithms solve problems in this form: maximize cT x subject to Ax = b, x ≥ 0, where b and c are given vectors and A is a given matrix. Of course, x is a vector. ampl converts a problem from its “natural” formulation to this paradigm and then hands it off to a solver. IMPORTANT: ...
Fast-Fourier Optimization
... Linear programming algorithms solve problems in this form: maximize cT x subject to Ax = b, x ≥ 0, where b and c are given vectors and A is a given matrix. Of course, x is a vector. ampl converts a problem from its “natural” formulation to this paradigm and then hands it off to a solver. IMPORTANT: ...
... Linear programming algorithms solve problems in this form: maximize cT x subject to Ax = b, x ≥ 0, where b and c are given vectors and A is a given matrix. Of course, x is a vector. ampl converts a problem from its “natural” formulation to this paradigm and then hands it off to a solver. IMPORTANT: ...
Lecture05_waves_and_discontinuities
... – Fourier coefficients for frequencies above N/2 are determined exactly from the first N/2+1. – Above N they are periodic and between N/2 and N reflect with the same amplitude and phase change of π. – The DFT allows us to transform N real values in the time domain into any number of complex values A ...
... – Fourier coefficients for frequencies above N/2 are determined exactly from the first N/2+1. – Above N they are periodic and between N/2 and N reflect with the same amplitude and phase change of π. – The DFT allows us to transform N real values in the time domain into any number of complex values A ...
Discrete time Fourier transform and its Properties
... Here the summation ranges over any consecutive N integers of x[n], where N is the period of the discrete time signal x[n]. Here equation (i) is called the Synthesis Equation and equation (ii) is called the Analysis Equation. Now since x[n] is periodic with period N; the Fourier series coefficients ...
... Here the summation ranges over any consecutive N integers of x[n], where N is the period of the discrete time signal x[n]. Here equation (i) is called the Synthesis Equation and equation (ii) is called the Analysis Equation. Now since x[n] is periodic with period N; the Fourier series coefficients ...
PPT - cs.rochester.edu
... I(x i)=||f i || p , and the Fourier coefficients of f i can be expressed using the Fourier coefficients of f fi (x)=f(x)-f(x+i) f i(x) =2f(x) ...
... I(x i)=||f i || p , and the Fourier coefficients of f i can be expressed using the Fourier coefficients of f fi (x)=f(x)-f(x+i) f i(x) =2f(x) ...
Interpolation on the unit circle
... Despite the complicated-looking formulas, we are again only using basic high-school algebra and writing even indices as 2k and odd ones as 2k + 1. Note that equation (10) outlines the computation of one DFT coefficient, aj+1 . The whole DFT computes all n coefficients {a1 , a2 , . . . , an }. The la ...
... Despite the complicated-looking formulas, we are again only using basic high-school algebra and writing even indices as 2k and odd ones as 2k + 1. Note that equation (10) outlines the computation of one DFT coefficient, aj+1 . The whole DFT computes all n coefficients {a1 , a2 , . . . , an }. The la ...
PDF file - UC Davis Mathematics
... Repeat (1)–(3) of (b) of Problem 4 with σ = 1, 0.1, 0.01. In addition, 4) Compare the speed of the decay of the Fourier coefficients of this function with these different values of σ; 5) Compare these decays with those of Problems 3 and 4. Which decays faster? Why? 6) Do they agree with the discreti ...
... Repeat (1)–(3) of (b) of Problem 4 with σ = 1, 0.1, 0.01. In addition, 4) Compare the speed of the decay of the Fourier coefficients of this function with these different values of σ; 5) Compare these decays with those of Problems 3 and 4. Which decays faster? Why? 6) Do they agree with the discreti ...
PPT - Jung Y. Huang
... The Huygens-Fresnel Principle: knowing the field at any plane, the field at any other plane can be expressed as a superposition of spherical waves originating from each point in the first plane. The Fresnel Approximation: for |r|<<|Dz|, the equations simplify. Fourier Optics: the propagation integra ...
... The Huygens-Fresnel Principle: knowing the field at any plane, the field at any other plane can be expressed as a superposition of spherical waves originating from each point in the first plane. The Fresnel Approximation: for |r|<<|Dz|, the equations simplify. Fourier Optics: the propagation integra ...
DSP_Test1_2006
... 1. (5%) Let x[n] = [n+1]+2[n]+ 3[ n1]+ 2[ n2]+ [ n3], and y[n] = 2[n+1]+[n]5[ n1] [ n2]+ 3[ n3]. Find their convolution x[n]y[n]. 2. To prove the property that time-domain convolution implies z-domain multiplication, let us consider x[n] and y[n] ( n ) that are two discrete ...
... 1. (5%) Let x[n] = [n+1]+2[n]+ 3[ n1]+ 2[ n2]+ [ n3], and y[n] = 2[n+1]+[n]5[ n1] [ n2]+ 3[ n3]. Find their convolution x[n]y[n]. 2. To prove the property that time-domain convolution implies z-domain multiplication, let us consider x[n] and y[n] ( n ) that are two discrete ...
Fast Fourier Transform
... To determine the running time of procedure Recursive-FFT, we note, that exclusive of the recursive calls, each invocation takes time Θ(n), where n is the length of the input vector.The recurrence for the running time is therefore T(n) = 2T(n/2) + Θ(n) = Θ(n log n) ...
... To determine the running time of procedure Recursive-FFT, we note, that exclusive of the recursive calls, each invocation takes time Θ(n), where n is the length of the input vector.The recurrence for the running time is therefore T(n) = 2T(n/2) + Θ(n) = Θ(n log n) ...
Discrete Fourier transform

In mathematics, the discrete Fourier transform (DFT) converts a finite list of equally spaced samples of a function into the list of coefficients of a finite combination of complex sinusoids, ordered by their frequencies, that has those same sample values. It can be said to convert the sampled function from its original domain (often time or position along a line) to the frequency domain.The input samples are complex numbers (in practice, usually real numbers), and the output coefficients are complex as well. The frequencies of the output sinusoids are integer multiples of a fundamental frequency, whose corresponding period is the length of the sampling interval. The combination of sinusoids obtained through the DFT is therefore periodic with that same period. The DFT differs from the discrete-time Fourier transform (DTFT) in that its input and output sequences are both finite; it is therefore said to be the Fourier analysis of finite-domain (or periodic) discrete-time functions.The DFT is the most important discrete transform, used to perform Fourier analysis in many practical applications. In digital signal processing, the function is any quantity or signal that varies over time, such as the pressure of a sound wave, a radio signal, or daily temperature readings, sampled over a finite time interval (often defined by a window function). In image processing, the samples can be the values of pixels along a row or column of a raster image. The DFT is also used to efficiently solve partial differential equations, and to perform other operations such as convolutions or multiplying large integers.Since it deals with a finite amount of data, it can be implemented in computers by numerical algorithms or even dedicated hardware. These implementations usually employ efficient fast Fourier transform (FFT) algorithms; so much so that the terms ""FFT"" and ""DFT"" are often used interchangeably. Prior to its current usage, the ""FFT"" initialism may have also been used for the ambiguous term ""finite Fourier transform"".