Download Trig Equations

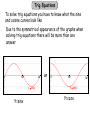
AS Use of Maths
Trig Equations
© Christine Crisp
Trig Equations
To solve trig equations you have to know what the sine
and cosine curves look like
Due to the symmetrical appearance of the graphs when
solving trig equations there will be more than one
answer
0
180
360 
y  sin x
Y=sinx
or
0
180
y  cos x
Y=cosx
360 
Trig Equations
Ex
Ex
Sin 45 = 0.7
And Sin 135 = 0.7
Cos 60 = 0.5
And Cos 300 = 0.5
0.7
0
0.5
45
135
180
360 
y  sin x
Y=sinx
0
60
180
y  cos x
Y=cosx
300
360 
Trig Equations
To solve trig equations use the forwards and
backwards method
Solve the equation
s in x  0  5
This means that if you find the sin of x then the
answer is 0.5
The opposite or inverse of sin x is sin–1x
Remember
an inverseinverse
function
function
This is pronounced
sinisxa and
is on which
the same
has
opposite
key the
as sin
x but effect
in yellow so use the 2nd F key
The inverse (opposite) of x2 is x
Trig Equations
Solve the equation
s in x  0  5
Forwards
x  sin it  = 0.5
Backwards
0.5  sin-1it  x
x = sin-10.5 = 30o
So the solution to the equation
sinx = 0.5 is
x = 30o
But unlike normal algebraic equations trig equations
have many answers because the trig graph is periodic
and repeats every 360o
Trig Equations
e.g.1 Solve the equation s in x  0  5.
Solution: The calculator gives us the solution x = 30 
BUT, by considering the graphs of y  s in x and y  0  5,
we can see that there are many more solutions:
y  s in x
y  05
30 
principal solution
Every point of intersection of y  s in x and y  0  5
gives a solution ! In the interval shown there are 10
solutions, but in total there are an infinite number.
The calculator value is called the principal solution
Trig Equations
We will adapt the question to:
Solve the equation s in x  0  5 for 0  x  360 
This limits the number of solutions
Solution: The first answer comes from the
calculator: Use the sin-1 key
Forwards
x  sin it  = 0.5
Backwards
0.5  sin-1it  x
x = sin-10.5 = 30o
Trig Equations
Sketch y  s in x between x  0 and x  360 
Add the line
y  05
There are 2
solutions.
1
0
-1
y  05
30

150

180 
360 
It’s important to show the scale.
y  s in x
Tip: Check that the solution from
the calculator
looks
The symmetry
of the graph
. .reasonable.
.
x  180  30  150
. . . shows the 2nd solution is
Trig Equations
e.g. 2 Solve the equation cos x   0  5 in the
interval 0  x  360 
Solution: The first answer from the calculator is
Forwards
x  cos it  = -0.5
Backwards
-0.5  cos-1it  x
x = cos-1-0.5 = 120o
The opposite or inverse of
cos x is cos–1x (inverse cos x)
Trig Equations
e.g. 2 Solve the equation cos x   0  5 in the
interval 0  x  360 
Solution: The first answer from the calculator is
Sketch
x  cos  1  0 . 5  120 
y  cos x between x  0 and x  360 
Add the line
y   05
There are 2
solutions.
1
0
-1
120 
180 
240 
y  cos x
360 
y   05
The symmetry of the graph . . .
. . . shows the 2nd solution is x  3 6 0  1 2 0  2 4 0 
Trig Equations
SUMMARY
 To solve s in x  c or c os x  c for 0  x  360 
where c is a constant
•
•
Find the principal solution from a calculator.
Sketch one complete cycle of the trig
function. For example sketch from 0  to 360.
180
0
360 
or
0
180
y  sin x
•
•
Draw the line y = c.
Find the 2nd solution using symmetry
y  cos x
360 
Trig Equations
Exercises
1. Solve the equations
(a) cos x  0  5 and (b) sin x 
Forwards
x  cos it  = 0.5
Backwards
0.5  cos-1it  x
x = cos-10.5 = 60o
3
2
for 0  x  360 
Trig Equations
Exercises
1. Solve the equations
(a) cos x  0  5 and (b) sin x 
Solution: (a) x  60 
3
2
for 0  x  360 
( from calculator )
1
y  05
0
60

180 
300 
y  cos x
-1
The 2nd solution is
x  36 0  6 0
 300 
360 
Trig Equations
Exercises
(b) s in x 
3
2
,
Forwards
x  sin it  =
0  x  360 
3
2
,
Backwards
3
 sin-1it  x
2
x = sin-1 3
2
= 60o
Trig Equations
Exercises
(b) s in x 
Solution:
3
2
,
x  60 
0  x  360 
( from calculator )
y
1
0
60 
120 
180 
The 2nd solution is
360 
y  s in x
-1
x  180  60
 120 
3
2
More Examples
Trig Equations
e.g. 5 Solve the equation s in x   0  5 for 0  x  360 
1
Using forwards and back
Solution: x  sin  0.5   30
y
1
 180 
 30 
180 
y   05
-1
330  x
360 
y  s in x
Since the period of the graph is 360 this solution . .
o
.. . . is
360  30  330
More Examples
Trig Equations
e.g. 5 Solve the equation s in x   0 . 5 for 0  x  360 
1
x

sin
 0.5   30
Solution:
y
1
 180 
210 
 30 
180 
y   05
-1
330  x
360 
y  s in x
Symmetry gives the 2nd value for 0  x  360
.


180  30  210 
The values in the interval 0  x  360  are 210 and 330
Trig Equations
e.g. 6 Solve cos x  0  4 for  180   x  360 
1
Solution: Principal value x  cos 0.4  66
Using forwards and back
Method
1
0
y  04
66 
180 
y  cos x
-1
By symmetry, x  3 6 0   6 6   2 9 4 
Ans:
66 , 294
294 
360 
Trig Equations
SUMMARY
 To solve s in x  c or c os x  c
• Find the principal value from the calculator.
•
Sketch the graph of the trig function showing
at least one complete cycle and including the
principal value.
•
•
Find a 2nd solution using the graph.
Once 2 adjacent solutions have been found, add
or subtract 360  to find any others in the
required interval.
Trig Equations
Exercises
1. Solve the equations ( giving answers correct to
the nearest whole degree )
(a) s in x   0  2
for
0  x  360
(b) co s x  0  6 5
for
0  x  360
Trig Equations
Exercises
(a) s in x   0  2 for
0  x  360
Solution: Principal value x   12 
y
Using forwards and back
1
192 
 12 
 180 
y   02
180 
-1
By symmetry,
348
360 
y  sin x
x  360  12  348
Ans:
x
192 , 348
Trig Equations
Exercises
(b) co s x  0  6 5 for
Solution: Principal value
0  x  360
x  cos 1 0.65  49
Using forwards and back
1
0
y  0  65
180 
49 
311 360
y  cos x
-1
x  360   49   311
Ans:
49 , 311

Trig Equations
Solve the following
(a) Sinx = 0.83
for
0  x  360
(b) Sinx = 0.49
for
0  x  360
(c) Cosx = 0.25
for
0  x  360
(d) Cosx = 0.65
for
0  x  360
Answers
a) 56.2o, 123.9
b) 29.3o, 150.7
b) 75.5o, 284.5
c) 49.5o, 310.5
Trig Equations