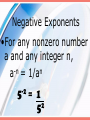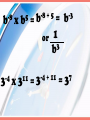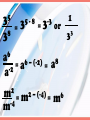Download 6.2 Law of Exponents / Scientific Notation

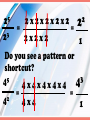
M8N1.
Students will understand
different representations of
numbers including
square roots, exponents, and
scientific notation.
Laws of Exponents
Scientific Notation
5 x 5 = 25
2
5
=
4
3
= 3 x 3 x 3 x 3 = 81
3
7
= 7 x 7 x 7 = 343
2
5
x
4
5
=
6
5
(5 x 5) (5 x 5 x 5 x 5)
Do you see a pattern or
shortcut?
3
3
x
5
3
=
8
3
(3x3x3)(3x3x3x3x3)
Do you see a pattern or
shortcut?
3
a
x
5
a
=
8
a
(a x a x a)(a x a x a x a x a)
Do you see a pattern or
shortcut?
Product of Powers Property
•To multiply powers
(exponents) with the
same base, add their
exponents.
3
+
2
5
a³ x a²= a
=a
5
2
3
2
=
2x2x2x2x2
2x2x2
=
2
2
1
Do you see a pattern or
shortcut?
5
3
4
4
4x4x4x4x4
=
=
2
4
4x4
1
Quotient of Powers Property
• To divide powers with the same
base, subtract the exponent of
the denominator from the
exponent of the numerator.
8
6
5
6
=
8-5
6
3
=6
REVIEW
•When multiplying- add
the exponents
•When dividing- subtract
the exponents.
EXAMPLES
3
2
9
6
4
6
•
2
=
2
= 65
5
2
7
b
•
3
b =
8
Z =
z3
10
b
5
z
Zero Exponents
•For any nonzero number a,
a0 = 1
•Anything to the zero power
equals 1 (except zero)
0
4
= 1
0
100
= 1
Negative Exponents
•For any nonzero number
a and any integer n,
-n
n
a = 1/a
-2
5
= 1
2
5
=1
5
3
-2
5 =1
2
5
-5
3
-2
3y
=3
2
y
-7
3
a b
=
3
b
7
a
-8
5
x
-3
5
=
-8
+
-3
5
or
-2
a
x
10
a
=
=
1
11
5
-2
+
10
a
=
-11
5
8
a
-8
b
x
5
b
=
-8
+
5
b
or
-4
3
x
11
3
=
=
1
3
b
-4
+
11
3
=
-3
b
7
3
5
3
=
8
3
6
a
5
8
3
=
-3
3
=
-2
a
6
–
(-2)
a
2
m
2
–
(-4)
m
=
m
=
-4
=
or
8
a
6
m
1
33
Scientific Notation
•is a short hand way of
writing numbers using
powers of 10
Standard
Notation
Product
Form
Scientific
Notation
1.2 x 108
120,000,000
1.2 x 100,000,000
Write in scientific notation.
9
4.62
x
10
46,200,000,000 =
Where is the decimal now?
Move the decimal to the
right of the first significant
digit.
Write in scientific notation.
89,000,000 =
8.9 x 107
Where is the decimal now?
Move the decimal to the
right of the first significant
digit.
Write in scientific notation.
11
3.04
x
10
304,000,000,000 =
Where is the decimal now?
Move the decimal to the
right of the first significant
digit.
Standard
Notation
Product
Form
Scientific
Notation
5.6 x 10-4
0.00056
5.6 x 0.0001
Write in scientific notation.
0.00000052 =
5.2 x 10-7
# is less than 1 so
exponent is negative
Move the decimal to the
right of the first significant
digit.
Write in scientific notation.
-9
1.06
x
10
0.00000000106 =
# is less than 1 so
exponent is negative
Move the decimal to the
right of the first significant
digit.
Write in standard form.
3.2 x
7
10 =
320 0 0 000
Count the # of spaces to
move and fill in with zeros.
Positive Exponents move the
decimal to the right
Write in standard form.
6.04 x
5
10 = 6
0 40 0 0
Count the # of spaces to
move and fill in with zeros.
Positive Exponents move the
decimal to the right
Write in standard form.
1.3 x
-5
10 =
0000 13
Count the # of spaces to
move left and fill in with
Negative
Exponents
move the
zeros.
Then
add a decimal
decimal
point to the left. # less than 1.
Write in standard form.
2.07 x
-4
10 =
0 0 0 207
Count the # of spaces to
move left and fill in with
Negative
Exponents
move the
zeros.
Then
add a decimal
decimal
point to the left. # less than 1.
Write these in scientific
notation.
4100
0.000067
62,000,000
0.000000003
4.1 x
3
10
6.7 x
-5
10
6.2 x
7
10
3x
-9
10
Write these in standard form.
3.04 x
7.2 x
5x
3
10
5
10
-3
10
3.8 x
-6
10
3,040
720,000
0.005
0.0000038