Download Lesson 4 Evaluation of Measurements

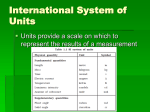
Homework
Read Pgs. 11-13
 Chapter 1 Problems 20, 24, 26,30
 Worksheet Scientific Measurement (2A
Extra Practice Problems)

Significant figures
Addition and Subtraction
 The
answer must have the
same number of decimal
places as the factor with the
least number of decimal
places.
Significant Figures
Example of Addition:
1250
+ 23.98
1273.98 (this is what a calculator will show)
1274 (this is the answer corrected for
significant figures, rounded to the 1’s place)
Significant figures
Multiplication and division
 The
answer must have the
same number of significant
figures as the factor with the
least number of significant
figures.
Significant figures
Example of Division:
15.375 / 5.0 = 3.075
(this is what a calculator will show)
Since the denominator only has 2
significant figures the answer is rounded
to 3.1
Significant Figures
8.654 m x 0.34 m =
 2.10 cm x 0.50 cm =

10.4815 ml ÷ 8.4 ml =
 0.365 m ÷ 0.050 m =

textbook HW
20a. 3
b. 4
c. 4
d. 1
e. 5
24a. 0.5
b. 401.4
c. 0.2684
d. 7.8
26a. 132.5 g
b. 298.69 cm
c. 13 lb
d. 350 oz
30. only c is exact
Scientific Measurement
1 a. 3
2 a. 133 g
e. 50.8 dm
b. 4
b. 109 mL
f. 2.86x103 cal
c. 7
c. 13 cm
d. 2
d. 14 g/mL
e. 3 f. 6
3 a. 1.0 e. 740.
4a. 145g e. 1.30x102dm
b. 40.1 f. 80
c. 6.2x10-5
d. 1.5
b. 64mL
f. 16 cm
c. 91.7 cm2 g. 6000cal
d. 4.3g/cm3
Unit 1
Read pages 8-9
 Unit 1 Sci. Notation and % Error
 Chapter 1 Problems 20, 24, 26,30
 Quiz: Oct 18/19 (Thursday / Friday)

Numbers and Measurement
Chemistry requires us to make accurate
measurements that are often very small
or very large.
 To more easily handle these very large
and small numbers, we use scientific
notation.

Scientific Notation

Measurements are written as the product
of two numbers
A coefficient – number between 1 and 10
 10 raised to a power – the exponent
indicates the number of times the coefficient
must be multiplied or divided by 10.

Scientific Notation

Write the following in scientific notation:
6,954,000
 175.983


Write the following in standard numerical
form:
6.75 x 10-3
 1.865 x 102

Calculations in Scientific Notation

Multiplication
Multiply coefficients
 Add exponents


Perform the following calculations:
7.2 x 102 · 5.02 x 10-3
 1.0 x 102 · 2.6 x 108

Calculations in Scientific Notation

Division
Divide coefficients
 Subtract the exponent of the denominator
from the exponent of the numerator.


Perform the following calculations:
8.4 x 103 / 2.1 x 10-2
 7.25 x 104 / 5.0 x 102

Calculations in Scientific Notation

Addition and subtraction
Make the exponent of both numbers the
same
 Align decimal points, and add coefficients
 The exponent of the result will be the same
as for the measurements

Calculations in Scientific Notation

Perform the following calculations:
1.
6.3 x 104 + 2.1 x 10-3
2.
7.563 x 102 - 1.77789 x 10-3
Calculations in Scientific Notation
1.
1.5 x 106 + 2.7 x 103
2.
6.38 x 10-3 – 3.8 x 10-4
International System of Units
Units of Measurement
Quantity
SI base unit or derived unit
Symbol
Length
meter
m
Volume
cubic meter
m3
Mass
kilogram
kg
Density
grams per cubic centimeter
g/cm3
Temperature
Kelvin
K
Time
second
s
Pressure
Pascal
Pa
Energy
joule
J
Amount of Substance
mole
mol
Luminous Intensity
candela
cd
Electric Current
ampere
a
SI Units









103 for kilo106 for mega109 for giga10-1 for deci10-2 for centi10-3 for milli10-6 for micro10-9 for nano10-12 for pico-
k
M
G
d
c
m
μ
n
p
Accuracy: Evaluations of
Measurements
Accepted
value: True or
correct value based on
reliable source
Experimental value:
measured by you during the
experiment
Error
 Difference
between the
accepted value and the
experimental value
 Take the absolute value
% Error
% Error = Error / accepted value * 100
% Error = Actual – Experimental x 100
Actual
What is the % error?

A student measures a volume as
25.0mL, whereas the correct volume is
23.2mL.
Density
Which is heavier – a
pound of popcorn or a
pound of cheese?
 They would have the
same mass!!
 However, if you had equal
VOLUMES of popcorn and
cheese, the cheese would
have more mass.

Density

A cube of gold-colored metal with a
volume of 64 cm3 has a mass of 980.
grams. The density of pure gold is 19.3
g/cm3. Is the metal pure gold?
Unit 1
HW: Read pages 9-10
 Unit 1: Density and Temperature
 More Conversion Problems

Temperature
The temperature of an object determines
the flow of heat transfer.
 Celsius scale uses the freezing point of
water as 0 and the boiling point of water
as 100.
 Kelvin scale uses 273 for the freezing
point of water, and 373 as the boiling
point.

(Gabriel) Fahrenheit Scale
 German
physicist
 Developed scale in 1714
 Hg was used in thermometer
 Freeze pt. water = 32˚F
 Boiling pt. water = 212˚F
 0˚F = freeze pt. of water, salt and
dry ice (CO2)
Why use Hg in a thermometer?
 For
every degree the mercury’s
temp. increases, the difference
in which the Hg expands is
NOTICABLE and CONSTANT.
 Alcohol thermometer used in
Alaska because Hg will freeze!
(Anders) Celsius Scale
 Developed
in 1742
 Swedish Astronomer
 Freezing pt. of water = 0˚C
 Boiling pt. of water = 100˚C
 Uses Hg in thermometer
9
F  C  32
5
(Lord William) Kelvin Scale
Developed in 1848
 Based on absolute zero = zero heat
energy = all motion stops
 0 Kelvin = -273.15˚C
 No degree on scale (Kelvin units)
 Kelvin is a theoretical scale because it
does not compare the temp. to FP or BP
of water.
 Based on lowest temperature possible –
No negative numbers on scale

Compare the 3 temperature scales