Download Do Now 9/29/06

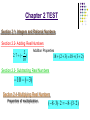
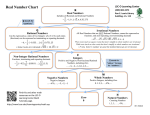
Do Now 9/23/11
What is the area for each figure?
What are the dimensions for each
figure?
Write an equation for area of the
figure?
A= 36
Can you think of an equation
for ONE side of the figure?
A= 16 A = 4²
6
4
4
6
A = 6²
Objective

find square roots, and compare real
numbers
Section 2.7 “Find Square
Roots and Compare Numbers”
If b² = a then
b is the square root of a.
The SQUARE ROOT of a number is
denoted by the symbol
, which
is called a radical.
9 3
radicand
Square Roots


All positive real numbers have two square roots, a
positive and negative square root.
The symbol  is read as “plus or minus” and
refers to both the positive and negative square
root.
 9  3
 16  4
100  10
The square of an integer is called a perfect square.
10  100
2
8  64
2
(9) 2  81
Not PERFECT???
10  ?
The square root of a whole number that is NOT a perfect
square is an IRRATIONAL
NUMBER.
numbers that cannot be written as a
quotient (fraction, ratio) of two integers
and the decimal neither terminates nor
repeats.
To find the square root of a
number that is not a perfect square
estimate or use a calculator to find the
square root.
10  3.162276601...
Evaluate each square root. Round your roots to
the nearest hundredth.
1) 841
2)  103
3)  6
2)  103
 10.15
3)  6
 2.45
SOLUTIONS
1) 841
 29
Use the
button on
your calculator for
square roots of numbers.
Approximate each square root to the nearest integer.
1) 80
2)  122
3)  3
2)  122
 11
3)  3
 2
SOLUTIONS
1) 80
9
To approximate a square, think
the closest perfect square to the
number under the radical sign.
“Real Numbers”
Rational Numbers
numbers that can
represented as a
ratio or fraction
a
,b  0
b
Real Numbers
Rational Numbers
Irrational Numbers
Integers
Irrational Numbers
√2 =1.414213…
Integers
-3,-2,-1, 0,1,2,3…
Whole Numbers
0,1,2,3,4,5…
Whole
Numbers
-√14=-3.74165…
Chapter 2 TEST
Section 2.1- Integers and Rational Numbers
Section 2.2- Adding Real Numbers
2
2 .7  (  )
10
Addition Properties
18  (2  3)  18  (3  2)
Section 2.3- Subtracting Real Numbers
 10  (3)
Section 2.4- Multiplying Real Numbers
Properties of multiplication
(8  3)  2  8  (3  2)
Chapter 2 Test
Section 2.5- The Distributive Property
Use the distributive property to write an equivalent expression
2(2x+7)
Section 2.6- Dividing Real Numbers
Simplify the expression
35  28 x
7
Section 2.7- Square Roots
 81