Download x - Savannah State University

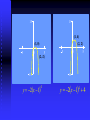
Sullivan PreCalculus
Section 3.2
Polynomial Functions
Objectives
• Identify Polynomials and Their Degree
• Graph Polynomial Functions Using Transformations
• Identify the Zeros of a Polynomial and Their Multiplicity
• Analyze the Graph of a Polynomial Function
A polynomial function is a function of the
form
f ( x )  a n x  a n 1 x
n
n 1
  a 1 x  a 0
where an , an-1 ,…, a1 , a0 are real numbers
and n is a nonnegative integer. The domain
consists of all real numbers. The degree of
the polynomial is the largest power of x that
appears.
Example: Determine which of the following are
polynomials. For those that are, state the degree.
(a) f ( x )  3x  4 x  5
2
Polynomial of degree 2
(b) h( x )  3 x  5
Not a polynomial
5
3x
(c) F ( x ) 
5  2x
Not a polynomial
A power function of degree n is a function
of the form
f ( x)  a n x
n
where a is a real number, a 0, and n > 0 is
an integer.
Summary of Power Functions with Even Degree
1.) Symmetric with respect to the y-axis.
2.) Domain is the set of all real numbers. Range is
the set of nonnegative real numbers.
3.) The graph always contains the points (0, 0);
(1, 1); and (-1, 1).
4.) As the exponent increases in magnitude, the
graph increases very rapidly as x increases, but for
x near the origin the graph tends to flatten out and
lie closer to the x-axis.
10
yx
8
8
yx
4
6
4
2
(-1, 1)
2
(1, 1)
1
(0, 0)
0
1
2
Summary of Power Functions with Odd Degree
1.) Symmetric with respect to the origin.
2.) Domain is the set of all real numbers. Range is
the set of all real numbers.
3.) The graph always contains the points (0, 0);
(1, 1); and (-1, -1).
4.) As the exponent increases in magnitude, the
graph becomes more vertical when x > 1 or x < -1,
but for -1 < x < 1, the graphs tends to flatten out
and lie closer to the x-axis.
10
yx
9
yx
6
2
(-1, -1)
1
5
2
(0, 0)
2
0
6
10
(1, 1)
1
2
Graph the following function using transformations.
f ( x )  4  2 x  1  2( x  1)  4
4
4
15
15
(1,1)
5
(0,0) 0
5
15
yx
(0,0)
5
0
(1, -2)
15
4
y  2 x 4
5
15
15
(1, 4)
(1,0)
5
0
(2, 2)
5
(2,-2)
0
5
15
15
y  2 x  1
5
4
y  2x 1  4
4
f ( x )  ( x  1)( x  4)
Consider the polynomial:
2
Solve the equation f (x) = 0
2
f ( x )  ( x  1)( x  4) = 0
x+1=0
OR
x-4=0
x=-1
OR
x=4
If f is a polynomial function and r is a real number
for which f (r) = 0, then r is called a (real) zero of
f, or root of f. If r is a (real) zero of f, then
a.) (r,0) is an x-intercept of the graph of f.
b.) (x - r) is a factor of f.
x  r 
m
m 1


x

r
is a factor of a polynomial f and
If
is not a factor of f, then r is called a zero of
multiplicity m of f.
Example: Find all real zeros of the following
function and their multiplicity.
5
1
2
f ( x )   x  3  x  7 x  

2
x = 3 is a zero with multiplicity 2.
x = - 7 is a zero with multiplicity 1.
x = 1/2 is a zero with multiplicity 5.
If r is a Zero of Even Multiplicity
Sign of f (x) does not
change from one side to
the other side of r.
Graph touches
x-axis at r.
If r is a Zero of Odd Multiplicity
Sign of f (x) changes
from one side to the
other side of r.
Graph crosses
x-axis at r.
Theorem: If f is a polynomial function of
degree n, then f has at most n - 1 turning
points.
Theorem: For large values of x, either
positive or negative, the graph of the
polynomial
f ( x )  a n x  a n 1 x
n
n 1
  a 1 x  a 0
resembles the graph of the power function
f ( x)  a n x
n
For the polynomial
2
f ( x )   x  1  x  5 x  4
(a) Find the x- and y-intercepts of the graph of f.
The x intercepts (zeros) are (-1, 0), (5,0), and (-4,0)
To find the y - intercept, evaluate f(0)
f (0)  (0  1)(0  5)(0  4)  20
So, the y-intercept is (0,-20)
For the polynomial
2
f ( x )   x  1  x  5 x  4
b.) Determine whether the graph crosses or touches
the x-axis at each x-intercept.
x = -4 is a zero of multiplicity 1 (crosses the x-axis)
x = -1 is a zero of multiplicity 2 (touches the x-axis)
x = 5 is a zero of multiplicity 1 (crosses the x-axis)
c.) Find the power function that the graph of f
resembles for large values of x.
f (x)  x
4
For the polynomial
2
f ( x )   x  1  x  5 x  4
d.) Determine the maximum number of turning points
on the graph of f.
At most 3 turning points.
e.) Use the x-intercepts and test numbers to find the
intervals on which the graph of f is above the x-axis and
the intervals on which the graph is below the x-axis.
On the interval    x   4
Test number:
x = -5
f (-5) = 160
Graph of f: Above x-axis
Point on graph: (-5, 160)
For the polynomial
2
f ( x )   x  1  x  5 x  4
On the interval  4  x   1
Test number:
x = -2
f (-2) = -14
Graph of f: Below x-axis
Point on graph: (-2, -14)
On the interval  1  x  5
Test number:
f (0) = -20
Graph of f:
x= 0
Below x-axis
Point on graph: (0, -20)
For the polynomial
2
f ( x )   x  1  x  5 x  4
On the interval 5  x  
Test number:
x=6
f (6) = 490
Graph of f: Above x-axis
Point on graph: (6, 490)
f.) Put all the information together, and connect the
points with a smooth, continuous curve to obtain the
graph of f.
500
(6, 490)
300
(-1, 0)
(-5, 160)
100
8
(-4, 0)
6
4
(0, -20)
2 0 2
100
(-2, -14)
300
4
(5, 0)
6
8