Download Multiply Rational Numbers

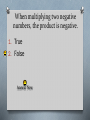
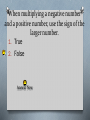
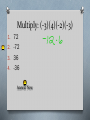
Lesson 2-6 and 2-7
Multiplying and Dividing Rational
Numbers
Objective
Students will be able to:
1.multiply rational numbers
2.divide rational numbers
Multiplying Rules
1) If the numbers have the same
signs then the product is positive.
(-7) • (-4) = 28
2) If the numbers have different
signs then the product is negative.
(-7) • 4 = -28
Examples
1) (3x)(-8y)
-24xy
2)
4 

20 
5
Write both numbers as a fraction.
Cross-cancel if possible.
 20 4 
 1 5 
Multiplying fractions:
80

5
top # • top #
= -16
Bottom # • bottom#
When multiplying two negative
numbers, the product is negative.
1. True
2. False
Answer Now
When multiplying a negative number
and a positive number, use the sign of the
larger number.
1. True
2. False
Answer Now
2
5




3) 

 5  8 
10
=
40
=
1
4
Multiply: (-3)(4)(-2)(-3)
1. 72
2. -72
3. 36
4. -36
Answer Now
an easy way to determine the sign of the answer
When you have an odd number of negatives,
the answer is negative.
When you have an even number of negatives,
the answer is positive.
4) (-2)(-8)(3)(-10)
Do you have an even or odd number of
negative signs?
3 negative signs -> Odd -> answer is negative
-480
Last one!
1
2



2
5)  65
 2 
 5 
Positive or negative answer?
Positive - even # of negative signs (4)
Write all numbers as fractions and multiply.
 1  6 52  2 
 2  1 1  5  1 
120
10
=12
Dividing Rules
(same as multiplication)
1) If the numbers have the same signs
then the quotient is positive.
-32 ÷ (-8 )= 4
2) If the numbers have different signs
then the quotient is negative.
81 ÷ (-9) = -9
When dividing two negative
numbers, the quotient is positive.
1.
2.
True
False
Answer Now
When dividing a negative number and a
positive number, use the sign of the
larger number.
1.
2.
True
False
Answer Now
a
b
The reciprocal of
is
b
a
where a and b  0.
The reciprocal of a number is called its
multiplicative inverse.
A number multiplied by its
reciprocal/multiplicative inverse is
ALWAYS equal to 1.
Example #1
7
2
The reciprocal of
is
.
7
2
2 7
1
 
1
7 2
1
Example #2

1
The reciprocal of -3 is  .
3
3
1
1
1

3

1
1
Basically, you are flipping the fraction!
We will use the multiplicative inverses
for dividing fractions.
Which statement is false about
reciprocals?
1.
2.
3.
4.
Reciprocals are also called
additive inverses
A number and its reciprocal
have same signs
If you flip a number, you get
the reciprocal
The product of a number
and its reciprocal is 1
Answer Now
Examples
1)  3  5
4
8
When dividing fractions, change division to
multiplying by the reciprocal.
3
8
24



20
4
5
6

5
3 
2)  1  
 
5
 10 
1  10 

 

5  3 
10

15
2

3
1.
2.
3.
4.
18
-18
7
-7
What is the quotient of
-21 ÷ -3?
Answer Now
1 10

?
5
3
1.
2.
3.
4.
2
3
2
3
3
50
3
50
.
.
.
.
Answer Now
Homework:
O Lesson 2-6
p. 109, 110 # 18-45
every 3rd
O Lesson 2-7
p. 115 # 15 -42
every 3rd