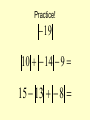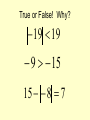* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Integer and Absolute value notes
Survey
Document related concepts
Transcript
Integers and
Absolute Value
Section 2-1
Intro to Integers
• An integer is the set of whole numbers
and their opposites, including zero,
represented by {… -3, - 2, - 1, 0, 1, 2,
3,…}
• A positive integer is a whole number
greater than zero.
• A negative integer is w whole number
less than zero.
• Website for Integer Rules
Things to remember
• Graph – means to draw a point on
the number line to represent the
integer.
• Zero is neither positive nor negative.
• Absolute value refers to the
distance away from zero an integer
is. (ALWAYS positive!)
How do I know if it is positive or
negative?
• Reference to zero.
• Ask yourself, “Is it good, did it help?”
• Look for key words:
–Negative: below, loss, withdraw, less
than, etc…
–Positive: above, profit, deposit, more
than, etc…
Absolute Value
• Key points for absolute value:
–Always positive because it refers
to distance from zero, not position
on the number line.
–Treat them like ( ). Solve the inside,
then take the absolute value.
–Simply remove the sign, keep the
number!
Practice!
19
10 14 9
15 13 8
Comparing and
Ordering
Integers
Section 2-2
How to read the signs
• < (less than)
• > (greater than)
• Example 1:
4<8
4 is less than 8
• Example 2:
– 5 > – 16
negative 5 is greater than
negative 16
Ordering Integers
• WARNING! graph or picture where
the negative numbers fall on a
number line.
• *It may be easier to think, “is this
negative number MORE negative
that one?”
True or False! Why?
19 19
9 15
15 8 7
Homework
• Worksheet
–Practice 2-2, All
–Skills Practice, Even