* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download MTH55A_Lec-10_sec_4
Big O notation wikipedia , lookup
List of important publications in mathematics wikipedia , lookup
Mathematics and architecture wikipedia , lookup
Mathematics and art wikipedia , lookup
Philosophy of mathematics wikipedia , lookup
History of mathematical notation wikipedia , lookup
Mathematics wikipedia , lookup
Principia Mathematica wikipedia , lookup
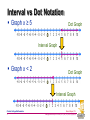
History of mathematics wikipedia , lookup
Critical mathematics pedagogy wikipedia , lookup
Foundations of mathematics wikipedia , lookup
Secondary School Mathematics Curriculum Improvement Study wikipedia , lookup
Chabot Mathematics §4.1 Solve InEqualities Bruce Mayer, PE Licensed Electrical & Mechanical Engineer [email protected] Chabot College Mathematics 1 Bruce Mayer, PE [email protected] • MTH55_Lec-14_sec_3-3a_3Var_Sys_Apps.ppt Review § 2.5 MTH 55 Any QUESTIONS About • §2.5 → Point-Slope Line Equation Any QUESTIONS About HomeWork • §2.5 → HW-7 Chabot College Mathematics 2 Bruce Mayer, PE [email protected] • MTH55_Lec-14_sec_3-3a_3Var_Sys_Apps.ppt Solving InEqualities An inequality is any sentence containing , , , , or . Some 3x 2 7, c 7, and 4x 6 3. Examples ANY value for a variable that makes an inequality true is called a solution. The set of all solutions is called the solution set. When all solutions of an inequality are found, we say that we have solved the inequality. Chabot College Mathematics 3 Bruce Mayer, PE [email protected] • MTH55_Lec-14_sec_3-3a_3Var_Sys_Apps.ppt Linear InEqualities A linear inequality in one variable is an inequality that is equivalent to one of the forms that are similar to mx + b ax b 0 or ax b 0 ax b 0 or ax b 0 where a and b represent real numbers and a ≠ 0. Chabot College Mathematics 4 Bruce Mayer, PE [email protected] • MTH55_Lec-14_sec_3-3a_3Var_Sys_Apps.ppt Example Chk InEqual Soln Determine whether 5 is a solution to a) 3x + 2 >7 b) 7x − 31 ≠ 4 SOLUTION a) Substitute 5 for x to get 3(5) + 2 > 7, or 17 >7, a true statement. Thus, 5 is a solution to InEquality-a b) Substitute to get 7(5) − 31 ≠ 4, or 4≠ 4, a false statement. Thus, 5 is not a solution to InEquality-b Chabot College Mathematics 5 Bruce Mayer, PE [email protected] • MTH55_Lec-14_sec_3-3a_3Var_Sys_Apps.ppt “Dot” Graphs of InEqualities Because solutions of inequalities like x < 4 are too numerous to list, it is helpful to make a drawing that represents all the solutions The graph of an inequality is such a drawing. Graphs of inequalities in one variable can be drawn on a number line by shading all the points that are solutions. Open dots are used to indicate endpoints that are not solutions and Closed dots are used to indicated endpoints that are solutions Chabot College Mathematics 6 Bruce Mayer, PE [email protected] • MTH55_Lec-14_sec_3-3a_3Var_Sys_Apps.ppt Example Graph InEqualities Graph InEqualities: a) x < 3, b) y ≥ −4; c) −3< x ≤ 5 Soln-a) The solutions of x < 3 are those numbers less than 3. • Shade all points to the left of 3 -4 -3 -2 -1 0 1 2 3 4 5 6 • The open dot at 3 and the shading to the left indicate that 3 is NOT part of the graph, but numbers such as 1 and −2 are Chabot College Mathematics 7 Bruce Mayer, PE [email protected] • MTH55_Lec-14_sec_3-3a_3Var_Sys_Apps.ppt Example Graph InEqualities Graph Inequalities: a) x < 3, b) y ≥ −4; c) −3< x ≤ 5 Soln-b) The solutions of y ≥ −4 are shown on the number line by shading the point for –4 and all points to the right of −4. • The closed dot at −4 indicates that −4 IS part of the graph -7 -6 -5 Chabot College Mathematics 8 -4 -3 -2 -1 0 1 2 Bruce Mayer, PE [email protected] • MTH55_Lec-14_sec_3-3a_3Var_Sys_Apps.ppt 3 Example Graph InEqualities Graph InEqualities: a) x < 3, b) y ≥ −4; c) −3< x ≤ 5 Soln-c) The inequality −3 < x ≤ 5 is read “−3 is less than x, AND x is less than or equal to 5.” -5 -4 -3 -2 -1 0 1 2 3 4 • Note the – OPEN dot at −3 → due to −3< x – CLOSED dot at 5 → due to x≤5 Chabot College Mathematics 9 Bruce Mayer, PE [email protected] • MTH55_Lec-14_sec_3-3a_3Var_Sys_Apps.ppt 5 Interval Notation Interval Notation for Inequalities on Number lines can used in Place of “Dot Notation: • Open Dot, → סLeft or Right, Single Parenthesis • Closed Dot, ● → Left or Right, Single Square-Bracket Chabot College Mathematics 10 Bruce Mayer, PE [email protected] • MTH55_Lec-14_sec_3-3a_3Var_Sys_Apps.ppt Interval vs Dot Notation Graph x ≥ 5 Dot Graph Interval Graph [ Graph x < 2 Dot Graph Interval Graph ) Chabot College Mathematics 11 Bruce Mayer, PE [email protected] • MTH55_Lec-14_sec_3-3a_3Var_Sys_Apps.ppt Interval Graphing of InEqualities If the symbol is ≤ or ≥, draw a bracket on the number line at the indicated number. If the symbol is < or >, draw a parenthesis on the number line at the indicated number. If the variable is greater than the indicated number, shade to the right of the indicated number. If the variable is less than the indicated number, shade to the left of the indicated number. Chabot College Mathematics 12 Bruce Mayer, PE [email protected] • MTH55_Lec-14_sec_3-3a_3Var_Sys_Apps.ppt Set Builder Notation In MTH55 the INTERVAL form is preferred for Graphing InEqualities A more compact alternative to InEquality Solution Graphing is SET BUILDER notation: x | x 3 SET BUILDER Notation Read as: “x such that x is… Chabot College Mathematics 13 Bruce Mayer, PE [email protected] • MTH55_Lec-14_sec_3-3a_3Var_Sys_Apps.ppt Compact Interval Notation Graphed Interval Notation can be written in Compact, ShortHand form by transferring the Parenthesis or Bracket from the Graph to Enclose the InEquality. Examples • x 13 → (−, 13 ] • −11< x 13 → (−11, 13] • −11< x → (−11, ) Chabot College Mathematics 14 Bruce Mayer, PE [email protected] • MTH55_Lec-14_sec_3-3a_3Var_Sys_Apps.ppt Example SetBuilder & Interval Write the solution set in set-builder notation and interval notation, then graph the solution set. a) x ≤ −2 b) n > 3 SOLUTION a) • Set-builder notation: {x|x ≤ −2} • Interval notation: (−, −2] • Graph Chabot College Mathematics 15 ] Bruce Mayer, PE [email protected] • MTH55_Lec-14_sec_3-3a_3Var_Sys_Apps.ppt Example Set Builder Write the solution set in set-builder notation and interval notation, then graph the solution set. a) x ≤ −2 b) n > 3 SOLUTION b) • Set-builder notation: {n|n > 3} • Interval notation: (3, ) • Graph Chabot College Mathematics 16 ( Bruce Mayer, PE [email protected] • MTH55_Lec-14_sec_3-3a_3Var_Sys_Apps.ppt Intervals on the Real No. Line Chabot College Mathematics 17 Bruce Mayer, PE [email protected] • MTH55_Lec-14_sec_3-3a_3Var_Sys_Apps.ppt Addition Principle for InEqs For any real numbers a, b, and c: • a < b is equivalent to a + c < b + c; • a ≤ b is equivalent to a + c ≤ b + c; • a > b is equivalent to a + c > b + c; • a ≥ b is equivalent to a + c ≥ b + c; Chabot College Mathematics 18 Bruce Mayer, PE [email protected] • MTH55_Lec-14_sec_3-3a_3Var_Sys_Apps.ppt Example Addition Principle Solve & Graph x 6 2 Solve (get x by itself) x66 26 x 4 Addition Principle Simplify to Show Solution Graph ( • Any number greater than −4 makes the statement true. Chabot College Mathematics 19 Bruce Mayer, PE [email protected] • MTH55_Lec-14_sec_3-3a_3Var_Sys_Apps.ppt Multiplication Principle for InEqs For any real numbers a and b, and for any POSITIVE number c: • a < b is equivalent to ac < bc, and • a > b is equivalent to ac > bc For any real numbers a and b, and for any NEGATIVE number c: • a < b is equivalent to ac > bc, and • a > b is equivalent to ac < bc Similar statements hold for ≤ and ≥ Chabot College Mathematics 20 Bruce Mayer, PE [email protected] • MTH55_Lec-14_sec_3-3a_3Var_Sys_Apps.ppt Mult. Principle Summarized Multiplying both Sides of an Inequality by a NEGATIVE Number REVERSES the DIRECTION of the Inequality • Examples 3x 6 2 3 3x 18 6 4x 1 x 101 4x 1 x 10 Chabot College Mathematics 21 Bruce Mayer, PE [email protected] • MTH55_Lec-14_sec_3-3a_3Var_Sys_Apps.ppt Example Solve & Graph Solve & Graph a) 4 y 20 Soln-a) 4 y 20 4 4 Graph y 5 1 b) x4 7 Divide Both Sides by −4 Reverse Inequality as the Eqn-Divisor is NEGATIVE ( The Solution Set: {y|y > −5} Chabot College Mathematics 22 Bruce Mayer, PE [email protected] • MTH55_Lec-14_sec_3-3a_3Var_Sys_Apps.ppt Example Solve & Graph 1 Soln-b) x 4 7 1 7 x 47 7 x 28 Multiply Both Sides by 7 Simplify Graph 5 5 10 10 15 15 20 20 25 25 The Solution Set: {x|x ≤ 28} Chabot College Mathematics 23 Bruce Mayer, PE [email protected] • MTH55_Lec-14_sec_3-3a_3Var_Sys_Apps.ppt ] 30 30 Example Add & Mult Principles Solve & Graph 4 x 1 x 10 SOLUTION 4 x 1 1 x 10 1 Add ONE to Both sides Simplify 4x x 9 Subtract x from Both Sides 4 x x x x 9 1 Divide Both Sides by 3 3x 9 3 x 3 Simplify & Show Solution ] Chabot College Mathematics 24 Bruce Mayer, PE [email protected] • MTH55_Lec-14_sec_3-3a_3Var_Sys_Apps.ppt Example Solve 3x − 3 > x + 7 Soln 3x 3 3 x 7 3 Add 3 to Both Sides 3x x 10 Simplify 3x x x x 10 Subtract x from Both Sides 2 x 10 Divide Both Sides by 2 2 Simplify x5 Graph -2 -1 0 1 2 3 4 ( 5 6 7 The Solution Set: {x|x > 5} Chabot College Mathematics 25 Bruce Mayer, PE [email protected] • MTH55_Lec-14_sec_3-3a_3Var_Sys_Apps.ppt 8 Example Solve 15.4 − 3.2x < −6.76 Soln 10015.4 3.2 x 6.76 To Clear Decimals 100 15.4 100 3.2 x 100 6.76 Dist. in the 100 1540 320x 676 Simplify 1540 1540 320x 676 1540 Subtract 1540 1 320 x 2216 Simplify; Mult. By −1/320 320 2216 x 6.925 Simplify; note that Inequality REVERSED by Neg. Mult. 320 The Solution Set: {x|x > 6.925} Chabot College Mathematics 26 Bruce Mayer, PE [email protected] • MTH55_Lec-14_sec_3-3a_3Var_Sys_Apps.ppt Example Solve & Graph Solve 5x 3 7 x 4x 3 9 Soln Use Distributive Law to 5x 15 7 x 4x 12 9 Clear Parentheses 2 x 15 4 x 3 Simplify 2x 15 3 4x 3 3 Add 3 to Both Sides 2x 12 4x Simplify 2x 2 x 12 2 x 4x Add 2x to Both Sides 1 Simplify; Divide 12 6 x Both Sides by 6 6 Chabot College Mathematics 27 Bruce Mayer, PE [email protected] • MTH55_Lec-14_sec_3-3a_3Var_Sys_Apps.ppt Example Solve & Graph Solve 5x 3 7 x 4x 3 9 1 Soln 12 6 x 2 x From Last Slide 6 x 2 Put x on R.H.S.; Note Reversed Inequality Graph -8 -7 -6 -5 -4 -3 ] -2 -1 0 1 The Solution Set: {x|x ≤ –2}. Chabot College Mathematics 28 Bruce Mayer, PE [email protected] • MTH55_Lec-14_sec_3-3a_3Var_Sys_Apps.ppt 2 Equation ↔ Inequality Equation Replace = by Inequality x=5 < x<5 3x + 2 = 14 ≤ 3x + 2 ≤ 14 5x + 7 = 3x + 23 > 5x + 7 > 3x + 23 x2 = 0 ≥ x2 ≥ 0 Chabot College Mathematics 29 Bruce Mayer, PE [email protected] • MTH55_Lec-14_sec_3-3a_3Var_Sys_Apps.ppt Terms of the (InEquality) Trade An inequality is a statement that one algebraic expression is less than, or is less than or equal to, another algebraic expression The domain of a variable in an inequality is the set of ALL real numbers for which BOTH SIDES of the inequality are DEFINED. The solutions of the inequality are the real numbers that result in a true statement when those numbers are substituted for the variable in the inequality. Chabot College Mathematics 30 Bruce Mayer, PE [email protected] • MTH55_Lec-14_sec_3-3a_3Var_Sys_Apps.ppt Terms of the (InEquality) Trade To solve an inequality means to find all solutions of the inequality – that is, the solution set. • The solution sets are intervals, and we frequently graph the solutions sets for inequalities in one variable on a number line • The graph of the inequality x < 5 is the interval (−, 5) and is shown here Chabot College Mathematics 31 ) 5 x < 5, or (–∞, 5) Bruce Mayer, PE [email protected] • MTH55_Lec-14_sec_3-3a_3Var_Sys_Apps.ppt Terms of the (InEquality) Trade A conditional inequality such as x < 5 has in its domain at least one solution and at least one number that is not a solution An inconsistent inequality is one in which no real number satisfies it. An identity is an inequality that is satisfied by every real number in the domain. Chabot College Mathematics 32 Bruce Mayer, PE [email protected] • MTH55_Lec-14_sec_3-3a_3Var_Sys_Apps.ppt THE NON-NEGATIVE IDENTITY x 0 2 for ANY real number x Because x2 = x•x is the product of either (1) two positive factors, (2) two negative factors, or (3) two zero factors, x2 is always either a positive number or zero. That is, x2 is never negative, or is always nonnegative Chabot College Mathematics 33 Bruce Mayer, PE [email protected] • MTH55_Lec-14_sec_3-3a_3Var_Sys_Apps.ppt Solving Linear InEqualities 1. Simplify both sides of the inequality as needed. a. Distribute to clear parentheses. b. Clear fractions or decimals by multiplying through by the LCD just as was done for equations. (This step is optional.) c. Combine like terms. 2. Use the addition principle so that all variable terms are on one side of the inequality and all constants are on the other side. Then combine like terms. 3. Use the multiplication principle to clear any remaining coefficient. If you multiply (or divide) both sides by a negative number, then reverse the direction of the inequality symbol. Chabot College Mathematics 34 Bruce Mayer, PE [email protected] • MTH55_Lec-14_sec_3-3a_3Var_Sys_Apps.ppt Example Solve InEquality Solve 8x + 13 > 3x − 12 SOLUTION 8x − 3x + 13 > 3x − 3x − 12 5x + 13 > 0 – 12 5x + 13 –13 > –12 – 13 Subtract 3x from both sides. Subtract 13 from both sides. 5x > −25 5 x 25 5 5 Divide both sides by 5 to isolate x. x > −5 Chabot College Mathematics 35 Bruce Mayer, PE [email protected] • MTH55_Lec-14_sec_3-3a_3Var_Sys_Apps.ppt Example Solve InEquality Solve 8x + 13 > 3x – 12 SOLUTION Graph for x > −5 ( SOLUTION SetBuilder Notation {x|x > −5} SOLUTION Interval Notation (−5, ) Chabot College Mathematics 36 Bruce Mayer, PE [email protected] • MTH55_Lec-14_sec_3-3a_3Var_Sys_Apps.ppt Example AirCraft E.T.A. An AirCraft is 150 miles along its path from Miami to Bermuda, cruising at 300 miles per hour, when it notifies the tower that The Twin-Turbo-Prop is now set on automatic pilot. The entire trip is 1035 miles, and we want to determine how much time we should let pass before we become concerned that the plane has encountered Bermuda-Triangle trouble Chabot College Mathematics 37 Bruce Mayer, PE [email protected] • MTH55_Lec-14_sec_3-3a_3Var_Sys_Apps.ppt Example AirCraft E.T.A. Familiarize • Recall the Speed Eqn: Distance = [Speed]·[time] • So LET t ≡ time elapsed since plane on autopilot Translate • 300t = distance plane flown in t hours on AutoPilot • 150 + 300t = plane’s distance from Miami after t hours on AutoPilot Chabot College Mathematics 38 Bruce Mayer, PE [email protected] • MTH55_Lec-14_sec_3-3a_3Var_Sys_Apps.ppt Example AirCraft E.T.A. Translate the InEquality for Worry Plane’s distance from Miami ≥ Distance from Miami to Bermuda 150 300t 1035 150 300t 150 1035 150 Chabot College Mathematics 39 Bruce Mayer, PE [email protected] • MTH55_Lec-14_sec_3-3a_3Var_Sys_Apps.ppt Example AirCraft E.T.A. Carry Out 300t 885 300t 885 300 300 t 2.95 State: Since 2.95 is roughly 3 hours, the tower will suspect trouble if the plane has not arrived in about 3 hours Chabot College Mathematics 40 Bruce Mayer, PE [email protected] • MTH55_Lec-14_sec_3-3a_3Var_Sys_Apps.ppt Example CellPhone $Budget You have just purchased a new cell phone. According to the terms of your agreement, you pay a flat fee of $6 per month, plus 4 cents per minute for calls. If you want your total bill to be no more than $10 for the month, how many minutes can you use? Chabot College Mathematics 41 Bruce Mayer, PE [email protected] • MTH55_Lec-14_sec_3-3a_3Var_Sys_Apps.ppt Example CellPhone $Budget Familiarize: Say we use the phone 35 min per month. Then the Expense $6 $0.04 35 min $7.4 month min month month Now that we understand the calculation LET • x ≡ CellPhone usage in minutes per month Chabot College Mathematics 42 Bruce Mayer, PE [email protected] • MTH55_Lec-14_sec_3-3a_3Var_Sys_Apps.ppt Example CellPhone $Budget Translate: Montly Plus Expense Minute To Be $10 Expense Less Than $6 0.04 x $10 4 Or, With 6 x 10 0.04 = 4/100 100 Chabot College Mathematics 43 Bruce Mayer, PE [email protected] • MTH55_Lec-14_sec_3-3a_3Var_Sys_Apps.ppt Example CellPhone $Budget Carry Out Chabot College Mathematics 44 Bruce Mayer, PE [email protected] • MTH55_Lec-14_sec_3-3a_3Var_Sys_Apps.ppt Example CellPhone $Budget Check: If the phone is used for 100 minutes, you will have a total bill of $6 + $0.04(100) or $10 State: If you use no more than 100 minutes of cell phone time, your bill will be less than or equal to $10. Chabot College Mathematics 45 Bruce Mayer, PE [email protected] • MTH55_Lec-14_sec_3-3a_3Var_Sys_Apps.ppt WhiteBoard Work Problems From §4.1 Exercise Set • 62 (ppt), 53, 72, 80 Working Thru a Linear InEquality Chabot College Mathematics 46 Bruce Mayer, PE [email protected] • MTH55_Lec-14_sec_3-3a_3Var_Sys_Apps.ppt P4.1-62 Write InEquality for Passion greater-than, or equal-to Intimacy Find Crossing Point Thus Ans [0,5) or { x x 5} Chabot College Mathematics 47 Bruce Mayer, PE [email protected] • MTH55_Lec-14_sec_3-3a_3Var_Sys_Apps.ppt All Done for Today Eric Heiden Won Five Gold Medals and Set Five Olympic Records at the 1980 Winter Olympics Chabot College Mathematics 48 Bruce Mayer, PE [email protected] • MTH55_Lec-14_sec_3-3a_3Var_Sys_Apps.ppt Chabot Mathematics Appendix r s r s r s 2 2 Bruce Mayer, PE Licensed Electrical & Mechanical Engineer [email protected] – Chabot College Mathematics 49 Bruce Mayer, PE [email protected] • MTH55_Lec-14_sec_3-3a_3Var_Sys_Apps.ppt