* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Mandelbrot Set
Survey
Document related concepts
Transcript
CS 4731: Computer Graphics
Lecture 5: Fractals
Emmanuel Agu
What are Fractals?
Mathematical expressions
Approach infinity in organized way
Utilizes recursion on computers
Popularized by Benoit Mandelbrot (Yale university)
Dimensional:
Line is one-dimensional
Plane is two-dimensional
Defined in terms of self-similarity
Fractals: Self-similarity
Level of detail remains the same as we zoom in
Example: surface roughness or profile same as we zoom in
Types:
Exactly self-similar
Statistically self-similar
Examples of Fractals
Clouds
Grass
Fire
Modeling mountains (terrain)
Coastline
Branches of a tree
Surface of a sponge
Cracks in the pavement
Designing antennae (www.fractenna.com)
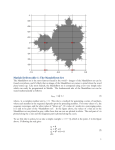
Example: Mandelbrot Set
Example: Mandelbrot Set
Example: Fractal Terrain
Courtesy: Mountain 3D
Fractal Terrain software
Example: Fractal Terrain
Example: Fractal Art
Courtesy: Internet
Fractal Art Contest
Application: Fractal Art
Courtesy: Internet
Fractal Art Contest
Koch Curves
Discovered in 1904 by Helge von Koch
Start with straight line of length 1
Recursively:
Divide line into 3 equal parts
Replace middle section with triangular bump with sides of
length 1/3
New length = 4/3
Koch Curves
S3, S4, S5,
Koch Snowflakes
Can form Koch snowflake by joining three Koch curves
Perimeter of snowflake grows as:
3
Pi 3 4
i
where Pi is the perimeter of the ith snowflake iteration
However, area grows slowly and S = 8/5!!
Self-similar:
zoom in on any portion
If n is large enough, shape still same
On computer, smallest line segment > pixel spacing
Koch Snowflakes
Pseudocode, to draw Kn:
If (n equals 0) draw straight line
Else{
Draw Kn-1
Turn left 60°
Draw Kn-1
Turn right 120°
Draw Kn-1
Turn left 60°
}
Iterated Function Systems (IFS)
Recursively call a function
Does result converge to an image? What image?
IFS’s converge to an image
Examples:
The Fern
The Mandelbrot set
The Fern
Mandelbrot Set
Based on iteration theory
Function of interest:
f ( z ) ( s) 2 c
Sequence of values (or orbit):
d1 ( s ) 2 c
d 2 (( s ) 2 c) 2 c
d 3 ((( s ) 2 c) 2 c) 2 c
d 4 (((( s ) 2 c) 2 c) 2 c) 2 c
Mandelbrot Set
Orbit depends on s and c
Basic question,:
For given s and c,
• does function stay finite? (within Mandelbrot set)
• explode to infinity? (outside Mandelbrot set)
Definition: if |s| < 1, orbit is finite else inifinite
Examples orbits:
s = 0, c = -1, orbit = 0,-1,0,-1,0,-1,0,-1,…..finite
s = 0, c = 1, orbit = 0,1,2,5,26,677…… explodes
Mandelbrot Set
Mandelbrot set: use complex numbers for c and s
Always set s = 0
Choose c as a complex number
For example:
• s = 0, c = 0.2 + 0.5i
Hence, orbit:
• 0,
c,
c 2,
c2+ c,
(c2+ c)2 + c, ………
Definition: Mandelbrot set includes all finite orbit c
Mandelbrot Set
Some complex number math:
i * i 1
For example:
2i * 3i 6
Modulus of a complex number, z = ai + b:
z a 2 b2
Squaring a complex number:
x yi ( x 2 y 2 ) (2 xy)i
Ref: Hill Appendix 2.3
Mandelbrot Set
Calculate first 4 terms
with s=2, c=-1
with s = 0, c = -2+i
Mandelbrot Set
Calculate first 3 terms
with s=2, c=-1, terms are
22 1 5
5 2 1 24
24 2 1 575
with s = 0, c = -2+i
0 (2 i) 2 i
(2 i) 2 (2 i) 1 3i
1 3i 2 (2 i) 10 5i
Mandelbrot Set
Fixed points: Some complex numbers converge to certain
values after x iterations.
Example:
s = 0, c = -0.2 + 0.5i converges to –0.249227 + 0.333677i
after 80 iterations
Experiment: square –0.249227 + 0.333677i and add
-0.2 + 0.5i
Mandelbrot set depends on the fact the convergence of
certain complex numbers
Mandelbrot Set
Routine to draw Mandelbrot set:
Cannot iterate forever: our program will hang!
Instead iterate 100 times
Math theorem:
if number hasn’t exceeded 2 after 100 iterations, never will!
Routine returns:
Number of times iterated before modulus exceeds 2, or
100, if modulus doesn’t exceed 2 after 100 iterations
See dwell( ) function in Hill (figure 9.49, pg. 510)
Mandelbrot Set
Map real part to x-axis
Map imaginary part to y-axis
Set world window to range of complex numbers to
investigate. E.g:
Choose your viewport. E.g:
X in range [-2.25: 0.75]
Y in range [-1.5: 1.5]
Viewport = [V.L, V.R, V.B, V.T]= [60,380,80,240]
Do window-to-viewport mapping
Mandelbrot Set
Mandelbrot Set
So, for each pixel:
Compute corresponding point in world
Call your dwell( ) function
Assign color <Red,Green,Blue> based on dwell( ) return
value
Choice of color determines how pretty
Color assignment:
Basic: In set (i.e. dwell( ) = 100), color = black, else color =
white
Discrete: Ranges of return values map to same color
• E.g 0 – 20 iterations = color 1
• 20 – 40 iterations = color 2, etc.
Continuous: Use a function
Mandelbrot Set
Use continuous function
FREE SOFTWARE
Free fractal generating software
Fractint
FracZoom
Astro Fractals
Fractal Studio
3DFract
References
Hill, chapter 9