* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Fractions_Priedas 3
Survey
Document related concepts
Transcript
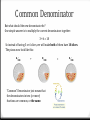
“Fruit fractions” Slice a pizza, and you will have fractions: 1/ 2 (One-Half) 1/ 4 (One-Quarter) 3/ 8 (Three-Eighths) The top number tells how many slices you have. The bottom number tells how many slices the pizza was cut into. Equivalent Fractions Some fractions may look different, but are really the same, for example: 4/ 8 = (FourEighths) 2/ 4 TwoQuarters) = 1/ = 2 (One-Half) = It is usually best to show an answer using the simplest fraction ( 1/2 in this case ). That is called Simplifying, or Reducing the Fraction. Numerator / Denominator We call the top number the Numerator, it is the number of parts you have. We call the bottom number the Denominator, it is the number of parts the whole is divided into. Numerator Denominator The denominator is the bottom number in a fraction. It shows how many equal parts the item is divided into You just have to remember those names! (If you forget just think "Down"ominator) Adding Fractions You can add fractions easily if the bottom number (the denominator) is the same: 1/ 1/ + 4 (OneQuarter) 2/ = 4 (OneQuarter) (TwoQuarters) + 1/ = 4 (One-Half) = = Another example: 5/ 8 + + 1/ 8 = = 6/ 8 2 = = 3/ 4 Adding Fractions Before you can add or subtract fractions, the fractions need to have a common denominator (in other words the denominators must be the same). 1. We multiplied each fraction by the denominator of the other. Let's use letters instead of numbers to show it: 2. And because they now have the same denominator, we can add them: We could do those two things in one step like this: Which you can use like this: (next slide) Example: What is 2/3 + 4/5 ? 2 4 + 3 2×5 + 3×4 = 5 10 + 12 = 3×5 (Note: "a" was 2, "b" was 3, "c" was 4 and "d" was 5.) 22 = 15 15 Common Denominator But what should the new denominator be? One simple answer is to multiply the current denominators together: 3 × 6 = 18 So instead of having 3 or 6 slices, we will make both of them have 18 slices. The pizzas now look like this: 6/ 18 + 3/ 18 "Common" Denominator just means that the denominators in two (or more) fractions are common, or the same. = 9/ 18 Adding Fractions with Different Denominators But what if the denominators (the bottom numbers) are not the same? As in this example: 3/ + 8 1/ = 4 + ? = You must somehow make the denominators the same. In this case it is easy, because we know that 1/4 is the same as 2/8 : 3/ 8 + + 2/ 8 = = 5/ 8 Subtracting Fractions There are 3 simple steps to subtract fractions: Step 1. Make sure the bottom numbers (the denominators) are the same. Step 2. Subtract the top numbers (the numerators). Put the answer over the same denominator. Step 3. Simplify the fraction. Example 1: 3 1 – 4 4 Step 1. The bottom numbers are already the same. Go straight to step 2. Step 2. Subtract the top numbers and put the answer over the same denominator: 3 1 3–1 – = 4 Step 3. Simplify the fraction: 4 1 = 4 = 4 2 2 2 4 Tasks 1. You Be the Designer. Use the four shapes you chose by your own and their colors (you can see the colors below) to design a figure on the triangle grid below. Calculate the fractional part of each color. 2. Determining the Relations. Answer the following questions. 3. Let's do some really fun ones. Calculate the shapes. 4. In the grid paper below draw your answers. Warning! These are a challenge, but fun to figure out! 5. Multiple Choice. Answer the questions and mark the correct answer. Homework Please, complete Task 6.