Download L3-Arithmetic - Peer Instruction for Computer Science

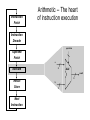
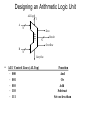
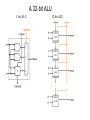
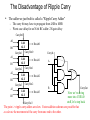
Reading – 4.1-4.3
Number Systems and Arithmetic
or
Computers go to elementary school
Peer Instruction Lecture Materials for Computer Architecture by Dr. Leo Porter is
licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0
Unported License.
What do all those bits mean now?
bits (011011011100010 ....01)
data
instruction
number
R-format
text chars
..............
I-format ...
integer
signed
...
unsigned
...
floating point
single precision
...
double precision
...
Questions About Numbers
• How do you represent
–
–
–
–
negative numbers?
fractions?
really large numbers?
really small numbers?
• How do you
– do arithmetic?
– identify errors (e.g. overflow)?
• What is an ALU and what does it look like?
– ALU=arithmetic logic unit
Two’s Complement Representation
• 2’s complement representation of negative numbers
– Take the bitwise inverse and add 1
• Biggest 4-bit Binary Number: 7
Smallest 4-bit Binary Number: -8
Decimal
-8
-7
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
7
Two’s Complement Binary
1000
1001
1010
1011
1100
1101
1110
1111
0000
0001
0010
0011
0100
0101
0110
0111
Point out negatives,
sign bit,
how to convert a 2’s
complement number
Some Things We Want To Know About Our
Number System
• negation
• sign extension
– +3 => 0011, 00000011, 0000000000000011
– -3 => 1101, 11111101, 1111111111111101
Introduction to Binary Numbers
Consider a 4-bit binary number
Decimal
Binary
Decimal
Binary
0
0000
4
0100
1
0001
5
0101
2
0010
6
0110
3
0011
7
0111
Walk through the add
Examples of binary arithmetic:
3+2=5
3+3=6
1
+
0
0
1
1
0
0
1
0
+
1
1
0
0
1
1
0
0
1
1
Can we use that same procedure for adding 2’s
complement negative #s as unsigned #s?
3+2 = 5
-5+-2 = -7
1
+
1
0
0
1
1
0
0
1
0
+
-1+2 = 1
1
1
1
0
1
1
1
1
1
0
+
1
1
1
1
1
1
0
0
1
0
Selection
“Best” Statement
A
Yes – the same procedure applies
B
Yes – the same “procedure” applies but it changes
overflow detection
C
No – we need a new procedure
D
No – we need a new procedure and new hardware
to implement it
E
None of the above
Overflow Detection
0
+
0
+
0
1
0
1
0
0
1
0
2
0
0
1
1
3
0
1
0
1
5
1
1
1
0
1
1
1
7
0
0
1
1
3
1
0
1
0
-6
+
1
+
So how do we detect overflow for signed arithmetic?
1
0
0
1
1
0
0
-4
1
1
1
0
-2
1
0
1
0
-6
0
1
0
1
1
0
0
-4
1
0
1
1
-5
0
1
1
1
7
2’s complement?
• We would like a number system that provides
–
–
–
–
–
–
obvious representation of 0,1,2...
uses adder for all addition
single value of 0
equal coverage of positive and negative numbers
easy detection of sign
easy negation
Two’s complement gives us this.
Instruction
Fetch
Arithmetic -- The heart
of instruction execution
Instruction
Decode
operation
Operand
Fetch
a
32
Execute
ALU
result
32
Result
Store
Next
Instruction
b
32
Designing an Arithmetic Logic Unit
ALUop
A
3
N
Zero
ALU
N
Result
Overflow
B
N
CarryOut
• ALU Control Lines (ALUop)
–
–
–
–
–
000
001
010
110
111
Function
And
Or
Add
Subtract
Set-on-less-than
A One Bit ALU
• This 1-bit ALU will perform AND, OR, and ADD
1
+
1
0
0
1
1
0
0
-4
1
1
1
0
-2
1
0
1
0
-6
A 32-bit ALU
1-bit ALU
32-bit ALU
Subtract – We’d like to implement a means of
doing A-B (subtract) but with only minor
changes to our hardware. How?
Explain “Provide an Option”.
1. Provide an option to use bitwise NOT A
2. Provide an option to use bitwise NOT B
3. Provide an option to use bitwise A XOR B
4. Provide an option to use 0 instead of the first CarryIn
5. Provide an option to use 1 instead of the first CarryIn
Selection
Choices
A
1 alone
B
Both 1 and 2
C
Both 3 and 4
D
Both 2 and 5
E
None of the above
Full ALU
ISOMORPHIC
what signals accomplish ADD?
Binvert CIn Oper
A
1
0
2
B
0
1
2
C
1
1
2
D
0
0
2
E
NONE OF THE ABOVE
sign bit (adder output from bit 31)
Full ALU
ISOMORPHIC
Careful – B is correct
but E isn’t that far off
what signals accomplish OR?
Binvert CIn Oper
A
1
0
0
B
0
1
1
C
1
1
0
D
1
0
1
E
NONE OF THE ABOVE
sign bit (adder output from bit 31)
Full ALU
Little more intense –
can you get this?
what signals accomplish SUB?
Binvert CIn Oper
A
1
0
2
B
0
1
2
C
1
1
2
D
0
0
2
E
NONE OF THE ABOVE
sign bit (adder output from bit 31)
Full ALU
Even harder….
Point out set bit is bit
31 from adder
Recall:
slt $t0, $t1, $t2
Means:
if($t1<$t2)
$t0 = 1
else
$t0 = 0
Which signals accomplish SLT
(assume A is in $t1, B in $t2)
(Note that the output “Set” is
always passed – what operation
ensures it is correct.)?
Binvert CIn Oper
A
1
0
2
B
0
1
2
C
1
1
3
D
0
0
3
E
NONE OF THE ABOVE
sign bit (adder output from bit 31)
Full ALU
For practice
what signals accomplish:
Binvert CIn Oper
add?
sub?
and?
or?
beq?
slt?
sign bit (adder output from bit 31)
The Disadvantage of Ripple Carry
• The adder we just built is called a “Ripple Carry Adder”
– The carry bit may have to propagate from LSB to MSB
– Worst case delay for an N-bit RC adder: 2N-gate delay
CarryIn0
A0
B0
A1
B1
A2
B2
A3
1-bit
Result0
ALU
CarryIn1 CarryOut0
1-bit
Result1
ALU
CarryIn2 CarryOut1
1-bit
Result2
ALU
CarryIn3 CarryOut2
1-bit
ALU
CarryIn
A
B
CarryOut
Now we’re diving
B3
more into CSE140
stuff, let’s step back
CarryOut3
The point -> ripple carry adders are slow. Faster addition schemes are possible that
accelerate the movement of the carry from one end to the other.
Result3
MULTIPLY HARDWARE
• 64-bit Multiplicand reg, 64-bit ALU, 64-bit Product reg,
32-bit multiplier reg
Here’s the hardware
to do multiply/divide,
they USE an adder
multiple times.
DIVIDE HARDWARE
• 64-bit Divisor reg, 64-bit ALU, 64-bit Remainder reg,
32-bit Quotient reg
Here’s the hardware
to do multiply/divide,
they USE an adder
multiple times.
You already know a way to write faster code.
Let’s say you have code which does: A = B*8.
What might you replace that code with to speed
up execution (which answer is best) by
leveraging faster hardware?
Selection
Choices
A
Do A = B+B+B+B+B+B+B+B
B
Do A = B sll 3
C
Do A = B sra 3
D
Do A = B srl 3
E
None of the above
Point out a compiler
might do this for you.
Floating-Point Numbers
Representation of floating point numbers in IEEE 754 standard:
1
8
23
sign
single precision
S
E
exponent:
excess 127
binary integer
(actual exponent is e = E - 127)
M
mantissa:
sign + magnitude, normalized
binary significand w/ hidden
integer bit: 1.M
Convert the following:
1 1000 0010 0100 0000 0000 0000 0000 000
Selection
Choices
A
- 1.010 * 2^130
B
-10
C
+10
D
1.010 * 2^130
E
None of the above
Need to be able to
convert both
directions.
FP Addition Hardware
Need to normalize –
the key here is this is
more complex than
Integer Add but not
as bad as, say, integer
multiply.
Modern Concerns
• Hardware designers have done an excellent job optimizing
multiply/FP hardware, but additions are still faster, than,
say multiply. Divides are even slower and have other
problems.
• More complex topics in later lectures will show how
multiply/FP/divide may not be on the “critical path” and
hence may not hurt performance as much as expected.
• More recent years have taught us that even “slow” multiply
is not nearly as important as cache/memory issues we’ll
discuss in later lessons.