Download Document

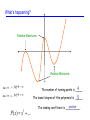
Analyzing Graphs
of Polynomials
Section 6.8
First a little review…
Given the polynomial function of the form:
f (x)  an xn  an1xn1    a1x  a0
If k is a zero,
x = k
Zero: __________
x = k
Solution: _________
(x – k)
Factor: _________
x - intercept
If k is a real number, then k is also a(n) __________________.
What kind of curve?
All polynomials have graphs that are smooth continuous curves.
A smooth curve is a curve that does not have sharp corners.
Sharp corner – This graph must not be
a polynomial function.
A continuous curve is a curve that does not have a break or hole.
Hole
Break
This is not a continuous curve!
End Behavior
An > 0 , Odd Degree
(Think of a line with
positive slope!)
An < 0 , Odd Degree
(Think of a line with
negative slope!)
y
y
x
An > 0 , Even Degree
(Think of a parabola
graph… y = x2 .)
y
y
x
An < 0 , Even Degree
(Think of a parabola
graph… y = -x2 .)
x
x
As x  -  , f(x)   As x  -  , f(x)  
As x  -  , f(x)   As x  -  , f(x)  
As x  +  , f(x)   As x  +  , f(x)  
As x  +  , f(x)   As x  +  , f(x)  
Examples of End Behaviors
x  , f ( x)  
1.
2.
x  , f ( x)  
x  , f ( x)  
x  , f ( x)  
3.
x  , f ( x)  
x  , f ( x)  
x  , f ( x)  
4.
x  , f ( x)  
What happens in the middle?
** This graph is said to have
3 turning points.
** The turning points happen when
the graph changes direction.
This happens at the vertices.
** Vertices are
minimums and maximums.
** The lowest degree of a polynomial is
(# turning points + 1).
So, the lowest degree of this
P( x)  x 4  ....
polynomial is
4!
What’s happening?
Relative Maximums
Relative Minimums
As x  -  , f(x)

As x  +  , f(x)

P( x)  x5  ....
4 .
The number of turning points is _____
The lowest degree of this polynomial is _____
5 .
positive
The leading coefficient is __________
.
Graphing by hand
Step 1: Plot the x-intercepts
Step 2: End Behavior? Number of Turning Points?
Step 3: Check in Calculator!!!
Negative-odd polynomial
of degree 3 ( -x * x * x)
f(x) = -(x + 4)(x + 2)(x - 3)
Example #1:
Graph the function:
and identify the following.
, f(x) 

As x  +
 , f(x)  
As x  - 
End Behavior: _________________________
3
Lowest Degree of polynomial: ______________
2
# Turning Points: _______________________
You can check on your calculator!!
x-intercepts
Graphing with a calculator
Example #2:
Graph the function:
and identify the following.
f(x) = x4 – 4x3 – x2 + 12x – 2
As x  -  , f(x)   As x  +  , f(x)  
End Behavior: _________________________
4
Degree of polynomial: ______________
3
# Turning Points: _______________________
(0, -2)
y-intercept: _______
Relative max
1. Plug equation into y=
Real Zeros
2. Find minimums and maximums
using your calculator
Relative minimum
Absolute minimum
Positive-even polynomial
of degree 4
Graphing without a calculator
Example #3:
Graph the function:
and identify the following.
f(x) = x3 - 3x2 – 4x


  As x  + 
End Behavior: _________________________
As x  -
, f(x)
, f(x)
3
Degree of polynomial: ______________
2
# Turning Points: _______________________
1. Factor and solve equation to find x-intercepts
f(x)=x(x2 - 3x – 4) = x(x - 4)(x + 1)
2. Plot the zeros. Sketch the end behaviors.
Positive-odd polynomial
of degree 3
Zero Location Theorem
Given a function, P(x) and a & b are real numbers.
If P(a) and P(b) have opposite signs, then there is at least one real
number c between a and b such that P(c) = 0.
a
b
P(b) is positive.
(The y-value is positive.)
Therefore, there must be at least
P(a) is negative.
(The y-value is negative.)
one real zero in between x = a & x = b!
Example #4: Use the Zero Location Theorem to verify that
P(x) = 4x3 - x2 – 6x + 1 has a zero between a = 0 and b = 1.
The graph of P(x) is continuous because P(x) is a polynomial function.
0
4 -1 -6 1
0 0 0
4 -1 -6 1
1
4 -1 -6 1
4 3 -3
4 3 -3 -2
P(0)= 1 and P(1) = -2  Furthermore, -2 < 0 < 1
The Zero Location Theorem indicates there is a real zero
between 0 and 1!
Polynomial Functions: Real Zeros, Graphs, and Factors (x – c)
• If P is a polynomial function and c is a real
root, then each of the following is equivalent.
is a factor of P
• (x – c) __________________________________
.
• x=c
is a real solution of P(x) = 0
__________________________________
.
• x=c
is a real zero of P
__________________________________
.
an x-intercept of the graph of y = P(x) .
• (c, 0) is
__________________________________
Even & Odd Powers of (x – c)
The exponent of the factor tells if that zero crosses over the x-axis or is a vertex.
If the exponent of the factor is ODD, then the graph CROSSES the x-axis.
If the exponent of the factor is EVEN, then the zero is a VERTEX.
Try it. Graph y = (x + 3)(x – 4)2
Try it. Graph y = (x + 6)4 (x + 3)3