Download Quadratic Functions

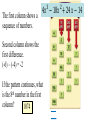
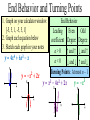
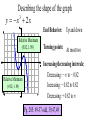
The first column shows a
sequence of numbers.
4𝑥 3 − 18𝑥 2 + 24𝑥 − 14
Second column shows the
first difference.
(-6) – (-4) = -2
If the pattern continues, what
is the 8th number in the first
column?
1074
5-1
Polynomial Functions
Unit Objectives:
• Solve polynomial equations
• Identify function attributes: domain, range, degree, relative
maximums/minimums, zeros
• Write and graph polynomial functions
• Model situations with polynomial functions
Today’s Objective:
I can describe polynomial functions.
Polynomial Function: Standard Form
Polynomial: sum of monomials (terms)
Degree of a polynomial: highest exponent
Standard form: terms arranged by exponents in descending order
𝑷 𝒙 = 𝒂𝒏 𝒙𝒏 + 𝒂𝒏−𝟏 𝒙𝒏−𝟏 + ⋯ + 𝒂𝟏 𝒙 + 𝒂𝟎
𝒂𝒏 𝒙𝒏 = Monomial
term
𝒂𝒏 = Coefficient
Real Number
𝒏 = Degree
Nonnegative
integer
Example: 𝑓 𝑥 = 4𝑥 3 + 3𝑥 2 + 5𝑥 − 2
Classifying Polynomial
By its Degree
Degree
3
Name
Constant
Linear
Quadratic
Cubic
4
Quartic
5
Quintic
n
nth degree
0
1
2
Examples
5
𝑥+3
3𝑥 2 + 4𝑥 + 5
3𝑥 3 + 𝑥 2 − 4𝑥 + 5
−7𝑥 4 + 𝑥 3 − 6𝑥 2 − 4𝑥 + 5
By the number of terms
# of terms
1
2
3
n
Name
Monomial
Binomial
Trinomial
polynomial
of n terms
𝑥 5 + 5𝑥 2
4𝑥 − 6𝑥 2 + 𝑥 4 + 10𝑥 2 − 12
Write in standard form.
Classify by degree & Terms
𝑥 4 + 4𝑥 2 + 4𝑥 − 12
quartic polynomial of 4 terms
End Behavior and Turning Points
1. Graph on your calculator window:
[-5, 5, 1, -5, 5, 1]
2. Graph each equation below
3. Sketch each graph in your notes
𝒚 = 𝟒𝒙𝟒 + 𝟔𝒙𝟑 − 𝒙
𝒚 = −𝒙𝟐 + 𝟐𝒙
End Behavior
Leading
Even
Odd
coefficient Degree Degree
a>0
↑ and ↑ ↓ and ↑
a<0
↓ and ↓ ↑ and ↓
Turning Points: At most n – 1
𝒚 = 𝒙𝟑 − 𝟒𝒙𝟐 + 𝟐𝒙
𝒚 = −𝒙𝟓
Describing the shape of the graph
3
y  x  2x
End Behavior:
Relative Maximum
(0.82, 1.09)
Up and down
Turning points: At most two
Increasing/decreasing intervals:
Relative Minimum
(-0.82, -1.09)
Decreasing: − ∞ to − 0.82
Increasing: − 0.82 to 0.82
Decreasing: + 0.82 to ∞
Pg. 285: #9-37 odd, 39,47,49