* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Quadratic Functions
Survey
Document related concepts
Transcript
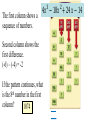
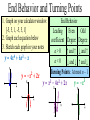
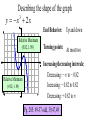
The first column shows a sequence of numbers. 4𝑥 3 − 18𝑥 2 + 24𝑥 − 14 Second column shows the first difference. (-6) – (-4) = -2 If the pattern continues, what is the 8th number in the first column? 1074 5-1 Polynomial Functions Unit Objectives: • Solve polynomial equations • Identify function attributes: domain, range, degree, relative maximums/minimums, zeros • Write and graph polynomial functions • Model situations with polynomial functions Today’s Objective: I can describe polynomial functions. Polynomial Function: Standard Form Polynomial: sum of monomials (terms) Degree of a polynomial: highest exponent Standard form: terms arranged by exponents in descending order 𝑷 𝒙 = 𝒂𝒏 𝒙𝒏 + 𝒂𝒏−𝟏 𝒙𝒏−𝟏 + ⋯ + 𝒂𝟏 𝒙 + 𝒂𝟎 𝒂𝒏 𝒙𝒏 = Monomial term 𝒂𝒏 = Coefficient Real Number 𝒏 = Degree Nonnegative integer Example: 𝑓 𝑥 = 4𝑥 3 + 3𝑥 2 + 5𝑥 − 2 Classifying Polynomial By its Degree Degree 3 Name Constant Linear Quadratic Cubic 4 Quartic 5 Quintic n nth degree 0 1 2 Examples 5 𝑥+3 3𝑥 2 + 4𝑥 + 5 3𝑥 3 + 𝑥 2 − 4𝑥 + 5 −7𝑥 4 + 𝑥 3 − 6𝑥 2 − 4𝑥 + 5 By the number of terms # of terms 1 2 3 n Name Monomial Binomial Trinomial polynomial of n terms 𝑥 5 + 5𝑥 2 4𝑥 − 6𝑥 2 + 𝑥 4 + 10𝑥 2 − 12 Write in standard form. Classify by degree & Terms 𝑥 4 + 4𝑥 2 + 4𝑥 − 12 quartic polynomial of 4 terms End Behavior and Turning Points 1. Graph on your calculator window: [-5, 5, 1, -5, 5, 1] 2. Graph each equation below 3. Sketch each graph in your notes 𝒚 = 𝟒𝒙𝟒 + 𝟔𝒙𝟑 − 𝒙 𝒚 = −𝒙𝟐 + 𝟐𝒙 End Behavior Leading Even Odd coefficient Degree Degree a>0 ↑ and ↑ ↓ and ↑ a<0 ↓ and ↓ ↑ and ↓ Turning Points: At most n – 1 𝒚 = 𝒙𝟑 − 𝟒𝒙𝟐 + 𝟐𝒙 𝒚 = −𝒙𝟓 Describing the shape of the graph 3 y x 2x End Behavior: Relative Maximum (0.82, 1.09) Up and down Turning points: At most two Increasing/decreasing intervals: Relative Minimum (-0.82, -1.09) Decreasing: − ∞ to − 0.82 Increasing: − 0.82 to 0.82 Decreasing: + 0.82 to ∞ Pg. 285: #9-37 odd, 39,47,49