Download Document

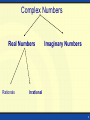
Section 2-2
Polynomial Functions
Zeros and Graphing
Objectives
• I can find real zeros and use them for
graphing
• I can determine the multiplicity of a zero
and use it to help graph a polynomial
• I can determine the maximum number of
turning points to help graph a polynomial
function
2
Complex Numbers
Real Numbers
Rationals
Imaginary Numbers
Irrational
3
A turning point of a graph of a function is a point at which the
graph changes from increasing to decreasing or vice versa.
A polynomial function of degree n has at most n – 1 turning
points and at most n zeros.
4
Degree (n)
• The degree of a polynomial tells us:
• 1. End behavior
– (If n is Odd) Ends in opposite directions
– (if n is Even) Ends in same direction
• 2. Maximum number of Real Zeros (n)
• 3. Maximum Number of Turning Points (n-1)
5
Example: Find all the real zeros and turning points of the graph
of f (x) = x 4 – x3 – 2x2.
Factor completely: f (x) = x 4 – x3 – 2x2 = x2(x + 1)(x – 2).
The real zeros are x = –1, x = 0, and x = 2.
y
These correspond to the
x-intercepts (–1, 0), (0, 0) and (2, 0).
The graph shows that
there are three turning points.
Since the degree is four, this is
Turning point
the maximum number possible.
Turning
point
x
Turning point
f (x) = x4 – x3 – 2x2
6
Repeated Zeros
If k is the largest integer for which (x – a) k is a factor of f (x)
and k > 1, then a is a repeated zero of multiplicity k.
1. If k is odd the graph of f (x) crosses the x-axis at (a, 0).
2. If k is even the graph of f (x) touches, but does not cross
through, the x-axis at (a, 0).
Example: Determine the multiplicity of the zeros
of f (x) = (x – 2)3(x +1)4.
y
Zero
2
Multiplicity Behavior
3 odd
crosses x-axis
at (2, 0)
–1
4 even
x
touches x-axis
at (–1, 0)
7
Multiplicity
• Multiplicity is how many times a solution is
repeated.
• First find all the factors to a given polynomial.
The exponents on each factor determine the
multiplicity.
• If multiplicity is ODD, the graph crosses the
solution
• If multiplicity is EVEN, the graph just touched or
bounces off the solution
8
Multiplicity
• (x+2)(x-3)2(x+1)3
• Zeros at (-2,0) (3, 0)
and (-1, 0)
• Crosses at (-2, 0)
• Touches (3, 0)
• Crosses (-1, 0)
9
Example: Sketch the graph of f (x) = 4x2 – x4.
1. Write the polynomial function in standard form: f (x) = –x4 + 4x2
The leading coefficient is negative and the degree is even.
as x  , f ( x )  
2. Find the zeros of the polynomial by factoring.
f (x) = –x4 + 4x2 = –x2(x2 – 4) = – x2(x + 2)(x –2)
Zeros:
x = –2, 2 multiplicity 1
x = 0 multiplicity 2
y
(–2, 0)
(2, 0)
x
(0, 0)
x-intercepts:
(–2, 0), (2, 0) crosses through
(0, 0)
touches only
Example continued
10
Putting it all together
• 1. Find degree and LC to determine end behavior,
maximum number of real zeros, and maximum
number of turning points
• 2. Find y-intercept
• 3. Factor and find all zeros
• 4. Determine multiplicity to determine if graph
crosses or touches at the zeros
• 5. Sketch the graph
11
f ( x)  x  x  2 x
4
Degree : 4
LC :1
3
2
End Behavior :  
4 possible zeros
3 possible turning points
Factors are: x ( x  1)( x  2)
2
Zeros are: (0,0), (1,0), (-2,0)
Touch
Cross
Cross
12
Homework
• WS 3-5
13