* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Solving problems with all operations
Survey
Document related concepts
Transcript
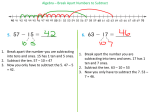
M4.A.2 Understand the meanings of operations, use operations and understand how they relate to each other. M4.A.2.1 Use operations to solve problems (may include word problems). M4.A.2.1 Eligible Content • M4.A.2.1.1 Solve problems involving all operations with whole numbers, and/or explain the solution (limit to two-step problems; e.g., multiply then add – single digit multipliers and divisors). • M4.A.2.1.2 Solve problems involving addition or subtraction with decimals through the tenths or money to the cent and/or explain the solution. Limit to two-step problems. M4.A.2.1.1 Solve problems involving all operations with whole numbers, and/or explain the solution (limit to two-step problems; e.g., multiply then add – single digit multipliers and divisors). PSSA Sample Item PSSA Sample Item PSSA Sample Item PSSA Sample Item PSSA Sample Item Addition • To add 723 and 246, first we add three six and _______. • To add 723 and 246, next we add two and _______. four • To add 723 and 246, next we add seven and _______. two Subtracting • Can we take one away from zero? No • To find the difference between 805 and 215, regroup next we _______ one hundred as ten tens. • To find the difference between 805 and 215, one next we take _______ away from ten. • To find the difference between 805 and 215, next we take _______ away from seven. two Multiplication • To solve 21 × 42, first we multiply the top number by the bottom number's _______ Ones value. • What is 2 × 2? 4 • Next, we multiply the top number by the bottom tens number's _______ value. • As we are multiplying by the _______ tens value, we must first place a zero to keep the place values lined up correctly. • When multiplying two two-digit numbers, product we write the second _______ below the first. We must make sure we line up the place values. • What is 4 × 1? 4 • What is 4 × 2? 8 products • Finally, we must add the _______. Division • To divide a two-digit number by a one-digit number, we must write the two-digit Right number to the _______ of the one-digit number. • What is a dividend? A number to be divided • What is a divisor A number that a dividend will be divided by. • What is a quotient? The result of a division sentence • What is a remainder? An amount left over after dividing two numbers. • First, we divide the dividend's tens value by the _______. Divisor • What is 6 ÷ 4? • 1 with a remainder • What is the first digit of the quotient? • 1 • After dividing the dividend's tens value by the multiply divisor, we _______ the divisor by the quotient's tens value. • What is 4 × 1? •4 • After multiplying the divisor by the quotient's tens value, we _______ subtract four from six. • After subtracting four from six, we bring down the dividend's _______ value. ones • After bringing down the dividend's ones value, we divide 20 by the _______. divisor • What is 20 ÷ 4? •5 • After we divide 20 by the multiply the divisor, we _______ divisor by the quotient's ones value. • What is 4 × 5? • 20 • After multiplying the divisor by the quotient's ones value, we _______ 20 from subtract 20. • What is 20 - 20? •0 • This quotient has no _______. Remainder Solving Word Problems Step 1 UNDERSTAND the problem. What are you trying to figure out? Here’s an example: Yesterday, Alex saw 14 birds in his backyard. Today, he saw 12. How many birds did he see in all? In this problem, what are you trying to figure out? If you said: “How many birds did Alex see in all?” then… You’re right! Step 2 Get a PLAN. How will you answer the question? Should you ADD or SUBTRACT? Look for clues. Here are some CLUE WORDS that will help you decide what to do. Addition Clue Words in all altogether sum total Subtraction Clue Words how many more how many are left difference Let’s look at the example again. Yesterday, Alex saw 14 birds in his backyard. Today, he saw 12. How many birds did he see in all? Do you see any CLUE WORDS? If you said… “in all,” then… You’re right! The words “in all” tell us that we should ADD! Now that we UNDERSTAND the problem, and have a PLAN, we’re ready for the next step! Step 3 SOLVE it! Write a number sentence using the information in the problem, and… Work it out! Give it a try! Yesterday, Alex saw 14 birds in his backyard. Today, he saw 12. How many birds did he see in all? Write a number sentence and SOLVE it. If you wrote… 14 + 12 = 26 then… You’re right! Step 4 LOOK BACK. Does your answer fit the question? We had to find out how many birds Alex saw in all. We added the number he saw yesterday and the number he saw today. Our answer was “Alex saw 26 birds in all.” It makes sense! Here are the steps once more: Step 1 – UNDERSTAND the problem. Step 2 – Get a PLAN. Step 3 – SOLVE it! Step 4 – LOOK BACK. Practice Word Problems 1. There are 11 crows perched on the branch of a tree. How many feet are there on the branch? • 11 x 2 = 22 feet 2. A starfish has 5 arms. How many arms do 6 starfish have? • 5 x 6 = 30 arms 3. There are 3 butterflies. Each butterfly has 4 black dots and 10 yellow dots. How many black dots are there in all? • 3 x 4 = 12 black dots 4. There are 2 lions and 5 tigers in a circus show. How many legs are there in all? • 5 + 2 = 7 4 legged animals 7 x 4= 28 legs 5. A magician has 6 hens. He makes each hen lay 5 eggs. How many eggs are there in all? • 6 x 5 = 30 eggs 1. There are 3 cakes. Each cake is cut into 7 parts. Each part is further cut into 3 pieces. How many cake pieces are there in all? • 3 x 7 = 21 21x 3 = 63 There are 63 pieces of cake in all. 2. The Professors at the State University drank 58 cups of tea yesterday. They drank 24 cups in the morning and 13 in the afternoon. How many did they drink in the evening? • 58-24= 34 cups left after the morning, 34-13= 21 cups left after the afternoon which leaves 21 cups of tea left to drink in the evening. 3. Brian borrowed 10 books from the school library. He returned 4 books yesterday and 4 books today. How many books does he still have? • 10- 4 = 6 books left after yesterday. 6-4= 2 books left after today. Which means he has 2 books left. 4. For her new kitchen, Mrs. Barbara bought a crockery set, a cutlery set and a pressure cooker. Each item cost $ 33 . How many dollars did she spend? • $33.00 x 3 items = $99.00 dollars. 5. There are 2 paintings on each of three walls of a room. If an art gallery has 5 such rooms, how many paintings are there in its collection? • 2 x 3= 6 paintings per room. 6 x 5= 30 paintings in the collection. M4.A.2.1.2 Solve problems involving addition or subtraction with decimals through the tenths or money to the cent and/or explain the solution. Limit to twostep problems. PSSA Sample Item PSSA Sample Item Essential Question: • • • • How do I add and subtract decimals? Always line up decimals Add and subtract like you always do Bring decimal straight down in your answers Adding Examples: 4.55 + 11.3 Put the first number on the top of the second number and line up the decimals. You can add a zero to help 4.55 keep + 11.30 everything lined up 15.85 When adding or subtracting you always start from the right and work left. 6.44 + 16 When there is not a decimal put one behind the number. Line up the decimal 6.44 + 16.0 22.44 Add a zero to line up everythin g Subtracting Examples: 5.34 -2.08 Put the first number on the top of the second number and line up the decimals. 5.34 -2.08 3.26 Different signs Take difference 28 – 15.911 When there is not a decimal put one behind the number. 7 99 28. 000 -15.911 1 2.0 8 9 Add zeros to line up everything, then subtract • What is 0.159 + 2.12? • Regrouping in addition, also known Carrying as _______, is putting a number from the tens place of a column answer into the next higher place value to the left. • What is 0.90 + 0.10? • Regrouping in subtraction, also known as borrowing is taking 1 from a column and _______, adding it as a unit of 10 to the column to the right. • What is 0.80 - 0.51? • What is 4.35 - 2.27? Adding and Subtracting Decimals When adding & subtracting numbers with decimals, stack the numbers on top of each other lining the decimals up. Remember, if a number doesn’t have a decimal, it comes at the end of the number. EX: 5.2 + 97.44 97.4 + 5.2 I can fill in empty spots with zeros. When I subtract, I have to fill in empty spots with 0’s. It’s not necessary with addition. • 722.8 + 0.2 722.8 + 0.2 723.0 ON ADDITION, you don’t have to fill in 0’s but you can. With SUBTRACTION, you need to fill in 0’s if the number is on top. EX: 8 – 2.54 8.0 - 2.5 5.5 • 75 – 0.24 - 75 0.2 (add a decimal & a couple 0’s) 75.0 - 0.2 74.8 Now try these: a) 10.4 - 0.2 c) 342.7 – 3.8 b) 100.3 – 20.4 d) 43 – 7.2 Now try these: a) 10.4 - 0.2 c) 342.7 – 3.8 b) 100.3 – 20.4 d) 43 – 7.2 First: line up the decimals 10.4 100.3 342.7 43.0 -0.2 -20.4 - 3.8 -7.2 10.2 79.9 338.9 35.8 • • • • • 72.3 – 4 89 – 42.3 44.2 – 39.6 66.2 – 44.9 Line up the decimals as shown below • These will all need 0’s added. • 72.3 89.0 44.2 66.2 - 4.0 -42.3 -39.6 -44.9 • These will all need 0’s added. • 72.3 89.0 44.2 66.2 - 4.0 -42.3 -39.6 -44.9 68.3 46.7 4.6 21.3 The veterinarian told Camilla that the mass of her puppy increased by 3.5 kg in the last month. If the puppy has a mass of 35.6 kg now, what was its mass a month ago? 35.6kg +3.5kg 39.1kg