* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Circuit Models for A..
Ground (electricity) wikipedia , lookup
Ground loop (electricity) wikipedia , lookup
Signal-flow graph wikipedia , lookup
Electrical ballast wikipedia , lookup
Immunity-aware programming wikipedia , lookup
Three-phase electric power wikipedia , lookup
Public address system wikipedia , lookup
Scattering parameters wikipedia , lookup
Variable-frequency drive wikipedia , lookup
Power inverter wikipedia , lookup
History of electric power transmission wikipedia , lookup
Negative feedback wikipedia , lookup
Audio power wikipedia , lookup
Electrical substation wikipedia , lookup
Distribution management system wikipedia , lookup
Power MOSFET wikipedia , lookup
Current source wikipedia , lookup
Integrating ADC wikipedia , lookup
Power electronics wikipedia , lookup
Alternating current wikipedia , lookup
Regenerative circuit wikipedia , lookup
Surge protector wikipedia , lookup
Two-port network wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Stray voltage wikipedia , lookup
Wien bridge oscillator wikipedia , lookup
Buck converter wikipedia , lookup
Voltage regulator wikipedia , lookup
Voltage optimisation wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Schmitt trigger wikipedia , lookup
Network analysis (electrical circuits) wikipedia , lookup
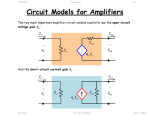
4/30/2017 582721780 1/10 Circuit Models for Amplifiers The two most important amplifier circuit models explicitly use the open-circuit voltage gain Avo : Iin Iout Zout Z in Vin Avo Vin Vout And the short-circuit current gain Ais : Iin Iout Vin Jim Stiles Zout Z in Ais Iin The Univ. of Kansas Vout Dept. of EECS 4/30/2017 582721780 2/10 In addition, each equivalent circuit model uses the same two impedance values—the input impedance Z in and output impedance Zout . Q: So what are these models good for? A: Say we wish to analyze a circuit in which an amplifier is but one component. Instead of needing to analyze the entire amplifier circuit, we can analyze the circuit using the (far) simpler equivalent circuit model. For example, consider this audio amplifier design: Vout Vin Jim Stiles The Univ. of Kansas Dept. of EECS 4/30/2017 582721780 3/10 Say we wish to connect a source (e.g., microphone) to its input, and a load (e.g., speaker) to its output: R1 L1 R2 Vg L2 Vout Let’s say on the EECS 412 final, I ask you to determine Vout in the circuit above. Q: Yikes! How could we possibly analyze this circuit on an exam—it would take way too much time (not to mention way too many pages of work)? A: Perhaps, but let’s say that I also provide you with the amplifier input impedance Z in , output impedance Zout , and open-circuit voltage gain Avo . You thus know everything there is to know about the amplifier! Just replace the amplifier with its equivalent circuit: Jim Stiles The Univ. of Kansas Dept. of EECS 4/30/2017 R1 Vg 582721780 4/10 L1 Zout Vin Z in R2 L2 Avo Vin Vout From input circuit, we can conclude (with a little help from voltage division): Zin Vin Vg R j ωL Z 1 in 1 And the output circuit is likewise: Vout R2 j ωL2 Avo Vin Zout R2 j ωL2 where: R2 j ωL2 j ω R2L2 R2 j ωL2 Q: Wait! I thought we could determine the output voltage from the input voltage by simply multiplying by the voltage gain Avo . I am certain that you told us: oc Vout Avo Vin Jim Stiles The Univ. of Kansas Dept. of EECS 4/30/2017 582721780 5/10 A: I did tell you that! And this expression is exactly correct. oc However, the voltage Vout is the open-circuit output voltage of the amplifier—in this circuit (like most amplifier circuits!), the output is not open! oc Hence Vout Vout , and so : R2 j ωL2 Vout Avo Vin Zout R2 j ωL2 R2 j ωL2 oc Vout Zout R2 j ωL2 oc Vout Now, combining the two expressions, we have our answer: Vout R2 j ωL2 Zout R2 j ωL2 Zin j ω R2L2 AvoVg R j ωL Z 1 in Z out R2 j ωL2 j ω R2L2 1 Zin Vg Avo R1 j ωL1 Zin Now, be aware that we can (and often do!) define a voltage gain Av , a value that is different from the open-circuit voltage gain of the amplifier. For instance, in the above circuit example we could define a voltage gain as the ratio of the input voltage Vin and the output voltage Vout : Jim Stiles The Univ. of Kansas Dept. of EECS 4/30/2017 582721780 Av 6/10 Vout Vin R2 j ωL2 Avo Zout R2 j ωL2 j ω R2L2 Avo Zout R2 j ωL2 j ω R2L2 Or, we could alternatively define voltage gain as the ratio of the source voltage Vg and the output voltage Vout : Av Vout Vg Zin Avo R1 j ωL1 Zin j ω R2L2 Z R j ωL j ω R L out 2 2 2 2 Q: Yikes! Which result is correct; which voltage gain is “the” voltage gain? A: Both are! We can define a voltage gain Av in any manner that is useful to us. However, we must make this definition explicit—precisely what two voltages are involved in the definition? No voltage gain Av is “the” voltage gain! Note that the open-circuit voltage gain Avo is a parameter of the amplifier—and of the amplifier only! Jim Stiles The Univ. of Kansas Dept. of EECS 4/30/2017 582721780 7/10 Contrast Avo to the two voltage gains defined above (i.e., Vout Vin and Vout Vg ). In each case, the result—of course—depends on amplifier parameters ( Avo , Zin , Zout ). However, the results likewise depend on the devices (source and load) attached to the amplifier (e.g., L1 , R1 , L2 , R2 ). The only amplifier voltage gain is its open-circuit voltage gain Avo ! Now, let’s switch gears and consider low-frequency (e.g., audio and video) applications. At these frequencies, parasitic elements are typically too small to have any practical significance. Additionally, low-frequency circuits frequently employ no reactive circuit elements (no capacitor or inductors). As a result, we find that the input and output impedances exhibit almost no imaginary (i.e., reactive) components: Zin ω Rin j 0 Zout ω Rout j 0 Likewise, the voltage and current gains of the amplifier are (almost) purely real: Jim Stiles The Univ. of Kansas Dept. of EECS 4/30/2017 582721780 8/10 Avo ω Avo j 0 Ais ω Ais j 0 Note that these real values can be positive or negative. The amplifier circuit models can thus be simplified—to the point that we can easily consider arbitrary time-domain signals (e.g., vin t or iout t ): iout t iin t Rout vin t Rin Avo vin t Jim Stiles vout t iout t iin t vin t Rin Rout Ais iin t The Univ. of Kansas vout t Dept. of EECS 4/30/2017 582721780 9/10 For this case, we find that the (approximate) relationships between the input and output are that of an ideal amplifier: v oc out t t A δ t t v t A vo in vo vin t i sc out t t A δ t t i t A i t is in is in Specifically, we find that for these low-frequency models: Rin Avo vin t iin t oc vout t vin t Rout Ais oc vout t sc iout t sc iout t iin t One important caveat here; this “low-frequency” model is applicable only for input signals that are likewise lowfrequency—the input signal spectrum must not extend beyond the amplifier bandwidth. Now one last topic. Frequently, both the input and output voltages are expressed with respect to ground potential, a situation expressed in the circuit model as: Jim Stiles The Univ. of Kansas Dept. of EECS 4/30/2017 582721780 10/10 iout t iin t Rout vin t Rin Avo vin t vout t Now, two nodes at ground potential are two nodes that are connected together! Thus, an equivalent model to the one above is: iout t iin t Rout vin t Rin Avo vin t vout t Which is generally simplified to this model: iout t iin t Rout vin t Jim Stiles Rin The Univ. of Kansas Avo vin t vout t Dept. of EECS