Download Distributions & Graphs - University of South Florida

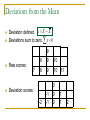
Central Tendency
Variables have distributions



A variable is something that changes or has
different values (e.g., anger).
A distribution is a collection of measures,
usually across people.
Distributions of numbers can be summarized
with numbers (called statistics or
parameters).
Central Tendency refers to the Middle of
the Distribution
Middle of the Distribution
(Common Statistics)

Mode


Median


Most common score
Top from bottom 50 percent
Mean

Arithmetic mean or average
Mode

The most frequently occurring score. Can
have bimodal and multimodal distributions.
Modal psychology student is female. Modal
number of pubs from grad school is zero.
p
Median


Score that separates top 50% from bottom
50%
Even number of scores, median is half way
between two middle scores.


1 2 3 4 | 5 6 7 8 – Median is 4.5
Odd number of scores, median is the middle
number

1 2 3 4 5 6 7 – Median is 4
Mean


Sum of scores divided by the number of
people. Population mean is  (mu) and
sample mean is X (X-bar).
We calculate the sample mean by:
X

X 
Raw score is X. N is number of people. Sigma
(Greek symbol like big E) is summation sign.
Add up scores and divide by the number of
people.
N

We calculate the population mean by:
X


N
Computation of Mean
X (scores)
Sum = 2+4+6 = 12
2
Mean = 12 / 3 = 4
4
6
 X  2  4  6  12
 X  12  4
N
3
Deviations from the Mean


Deviation defined. x  X  X
Deviations sum to zero.  x  0
9


Raw scores:
7
8
9
10
8
9
10
11
-1
-1
0
0
0
1
1
Deviation scores:
-2
2
Comparison of stats (1)

Mode



Good for nominal variables
Good if you need to know most frequent
observation
Quick and easy
Comparison of stats (2)
Median



Good for “bad” (skewed) distributions
Good for distributions with arbitrary ceiling or floor
Often used with distributions of money
Comparison of stats (3)

Mean




Used for inference as well as description; best
estimator of the parameter
Based on all data in the distribution
Generally preferred except for “bad” distribution.
Most commonly used statistic for central
tendency.
Effects of Distribution Shape
Review




What is central tendency?
Mode
Median
Mean
Computation


Consider the following scores: 1, 2, 2, 3, 3,
3, 4, 5
For the above set of scores, what is N?




Cannot be determined
2
3
8
Computation


Consider the following scores: 1, 2, 2, 3, 3,
3, 4, 5
For the above set of scores, what is the
percentage (relative frequency) of 2s?




2
10
20
25
Computation


Consider the following scores: 1, 2, 2, 3, 3,
3, 4, 5
For the above set of scores, what is the
mode?




2
3
4
5
Discussion Questions


Name a variable where it would be better to
find the median than the mean.
Why is it misleading to say that the average
person has 1.2 brothers? Why might it be
useful or helpful to say it anyway?