* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Significant Figures - Ramsey Public School District
Survey
Document related concepts
Transcript
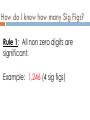
SIGNIFICANT FIGURES What is a significant figure? There are 2 kinds of numbers: 1. 2. Exact: Known with certainty. Example: the number of students in this room Approximate: anything MEASURED. Example: Mass, volume, length, weight, height No measurement is perfect. When to use Significant figures When a measurement is recorded only those digits that are dependable are written down. When to use Significant figures If you measured the width of a paper with your ruler you might record 21.7cm. To a mathematician 21.70, or 21.700 is the same. But, to a scientist 21.7cm and 21.70cm is NOT the same 21.700cm to a scientist means the measurement is accurate to within one thousandth of a cm. But, to a scientist 21.7cm and 21.70cm is NOT the same If you used an ordinary ruler, the smallest marking is the mm, so your measurement has to be recorded as 21.70cm. How do I know how many Sig Figs? Rule 1: All non zero digits are significant. Example: 1,246 (4 sig figs) How do I know how many Sig Figs? Rule 2: Any zeros between significant digits are also significant. Example: 1,206 (4 sig figs) How do I know how many Sig Figs? Rule 3: If the number does not contain a decimal point, any zeros to the right of a nonzero number are NOT significant Example: 1,200 (2 sig figs) How do I know how many Sig Figs? Rule 4: If zeros are at the end of a number that has a decimal, the zeros are significant. Example: 1,200. (4 sig figs) How do I know how many Sig Figs? Rule 5: If a value has no significant digits to the left of a decimal point, any zeros to the right of the decimal point before the non zero numbers (leading zeros) are not significant. Example: 0.0012 (2 sig figs) How do I know how many Sig Figs? Rule 6: Zeros that are found after non zero numbers to the right of a decimal point are significant (trailing zeros) Example: 0.1200 (4 sig figs) How do I know how many Sig Figs? When using scientific notation, all of the sig figs and ONLY the sig figs appear in the coefficient. 1.00 x 105 has 3 sig figs How many sig figs? 7 40 0.5 0.00003 7 x 105 7,000,000 1 1 1 1 1 1 How many sig figs here? 1.2 2100 56.76 4.00 0.0792 7,083,000,000 2 2 4 3 3 4 How many sig figs here? 3401 2100 2100.0 5.00 0.00412 8,000,050,000 6.02 x 10-23 4 2 5 3 3 6 3 What about calculations with sig figs? Rule: Addition/Subtraction When adding or subtracting measured numbers, the answer can have no more places after the decimal than the LEAST of the measured numbers. Add/Subtract examples 2.45cm + 1.2cm = 3.65cm round to = 3.7cm 7.432cm + 2cm = 9.432 cm round to 9cm Multiplication and Division Rule: multiplication/division When multiplying or dividing, the result can have no more significant figures than the least reliable measurement. A couple of examples 56.78 cm x 2.45cm = 139.111 cm2 round to 139cm2 75.8cm x 9.60cm = ? 728 cm2 Have Fun Measuring and Happy Calculating!