Download Math 50 - University of Wisconsin–Stout

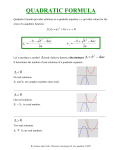
Please CLOSE YOUR LAPTOPS,
and turn off and put away
your cell phones,
and get out your note-taking
materials.
Today’s daily quiz will be
given at the end of the hour.
Section 11.2
The Quadratic Formula
Remember the problem like this one you had to solve
by factoring in the homework back in Chapter 6?
• Since there’s no GCF that we can take out, we can either “guess and check”
(which is harder than usual because there are so many possible combinations to
try), or we can use the British method.
• Even that method is a challenge, since it starts with multiplying 12*(-72) = -864,
then trying to find two factors of -864 that add up to 5.
• The factors that work are 32 and -27, so you’d have 12x2 +32x – 27x -72 = 0.
• Factoring by grouping then gives the correct factoring: (4x – 9)(3x + 8) = 0,
which leads to the two solutions of 9/4 and -8/3.
Wouldn’t it be nice if there was an easier
way to do this problem than by factoring?
The Quadratic Formula
The quadratic formula is another technique we
can use for solving quadratic equations.
Remember, quadratic equations are polynomial
equations of degree 2, such as
x2 + 3x -7 = 0
or
5x2 – 14 = 0.
The quadratic formula is derived from a process
called “completing the square” for a general
quadratic equation.
– See Section 11.1 in the online textbook if you’re
interested in seeing how this formula is derived.
– If you are taking Math 120 next, this will be
covered in that class in more detail, along with
the technique called “completing the square”.
The Quadratic Formula:
The two solutions to the equation
ax2 + bx + c = 0
(where a is the coefficient of the x2 term, b for the x term, and c is the constant term.)
are given by the formula
 b  b  4ac
x
2a
2
Notes:
1. The symbol ± means “plus or minus”.
2. Using the + version gives you one solution, and using the ˗ version
gives you the second solution.
3. This formula IS on the formula sheet, but you’ll probably have it
memorized by the time you’ve done the first few homework problems.
Example 1
Solve x2 + 4x + 3 = 0 by
• Factoring
• The quadratic formula.
Which way works best?
Solve x2 + 4x + 3 = 0 by factoring:
This one is pretty easy to factor.
The factoring is (x + 3)(x + 1) = 0,
so the solutions are given by
x + 3 = 0,
giving x = -3,
and x + 1 = 0,
giving x = -1.
Now, solve x2 + 4x + 3 = 0 by the quadratic formula:
a = 1, b = 4, c = 3, so the formula gives:
 4  4 2  4 1  3  4  16  12
x

2 1
2
4 4 42 42 2




 1
2
2
2
2
42 6
or

 3
2
2
Which way works best for this problem?
In this case, the factoring method is much quicker,
although BOTH methods give the same answer.
And by the way,
how would we check these answers
on a quiz or a test?
Back to this problem:
We’ve seen that factoring using the British method is a lot
of work. Let’s try using the quadratic formula instead.
Write the steps for this problem in your notebook
while I work it on the board.
(We’ll probably want to use a calculator to do the
multiplications in this problem.)
Answers: -8/3, 9/4
Example:
Solve x2 + 5x + 12 = 0 by
• Factoring
• The quadratic formula.
Which way works best?
Solve x2 + 5x + 12 = 0 by factoring:
This one looks pretty easy to factor, but when you
start trying to find two factors of 12 that add up to
5, nothing works.
(1+12=13, 2+6=8, 3+4=7).
What does this mean?
It means that the polynomial is PRIME, and there
are no rational solutions. (Remember, a rational
number is either an integer or a fraction.)
If you think a polynomial is prime, a good way to check is
by calculating the discriminant (the b2 – 4ac part under the
radical in the quadratic formula).
• If the discriminant is negative, then you know for sure that your
polynomial is prime and there are no real solutions. (There will be two
complex but not real solutions involving the square root of -1, which is given the
symbol “ i ”.)
• If the discriminant is positive and a perfect square, then you will
get two real solutions that are real and rational numbers.
• If the discriminant is positive but not a perfect square, then you
know for sure that your polynomial is prime (can’t be factored
without using radicals), but there will be two irrational solutions
that will contain radicals.
• If the discriminant is zero, there is only one real solution, and the
two factors of the quadratic trinomial will be the same binomial.
Solve x2 + 5x + 12 = 0 (continued):
• Let’s see what the quadratic formula gives in this case:
a = 1, b = 5, c = 12
so the formula gives:
 5  52  4 112  5  25  48  5   23
x


2 1
2
2
Notice that the number under the radical sign is negative,
which means there are no real answers.
There will be two complex but not real solutions involving
the symbol “ i ” which is the square root of -1.
Example:
Solve x2 + 2x - 4 = 0 by
• Factoring
• The quadratic formula.
Which way works best?
Solve x2 + 2x - 4 = 0 by factoring:
Again, this one looks like it would be easy to factor,
but when you start trying to find two factors of 4
that add up to 2, nothing works.
(-1 + 4 = 3, -4 + 1=-3, -2+2 = 0)
What does this mean?
It means that the polynomial is PRIME, and there
are no rational solutions. (Remember, a rational
number is a real number that is either an integer or
a fraction.)
Solve x2 + 2x - 4 = 0 (continued):
• Let’s see what the quadratic formula gives in this case:
a = 1, b = 2, c = -4
so the formula gives:
 2  2 2  4 1(4)  2  4  16  2  20
x


2 1
2
2
Notice that the number (20) under the radical sign is
positive, which means there are two real answers. However,
since 20 is not a perfect square, its square root is irrational.
In this case, we’d again say that the polynomial is prime,
because it has no rational roots.
Solve x2 + 2x - 4 = 0 using the quadratic formula (continued):
 2  2 2  4 1(4)  2  4  16  2  20
x


2 1
2
2
• IMPORTANT NOTE: Because the discriminant (20) is POSITIVE,
we still do have two REAL NUMBER solutions, but they won’t be
rational numbers because 20 is not a perfect square.
• If we are asked to find EXACT answers, that means we have to use
radicals in the answer, but first we need to check to see if the radical
can be simplified.
Can we simplify 𝟐𝟎?
Yes: 20 = 4*5 = 2*2*5 = 22*5
So 𝟐𝟎 =
22∗5 = 𝟐 𝟓
−𝟐 ±𝟐 𝟓
So our answers will be
𝟐
−𝟏 ±𝟏 𝟓
which simplifies to
, or -1+ 𝟓 , −1− 𝟓
𝟏
,
Solve x2 + 2x - 4 = 0 using the quadratic formula (continued):
 2  2 2  4 1(4)  2  4  16  2  20
x


2 1
2
2
What if, instead of being asked for an EXACT answers (-1+ 𝟓 ,
−1− 𝟓) to this equation, you were asked to find the approximate
solutions of this equation rounded to the nearest hundredth?
In this case, you could use your calculator to estimate 5 .
Do this now and see what you get for your two answers.
Answers: x = 1.24 and x = -3.24.
(How would you check this? Will you get EXACTLY zero?)
Question: What if some coefficients in your
quadratic equation are fractions?
ANSWER: Clear them first by multiplying all terms by the LCD:
1 2
5
Solve x + x – = 0 by the quadratic formula.
8
2
Step 1: Multiply every term by 8 to get
x2 + 8x – 20 = 0
Therefore a = 1, b = 8, c = -20
 8  (8)  4(1)( 20)  8  64  80  8  144
x



2
2
2(1)
2
 8  12

2
+ version gives: 4/2 = 2
- version gives -20/2 = -10
IMPORTANT:
When you check these answers,
plug them back into the ORIGINAL
equation, the one with the fractions,
just in case you made a mistake
when you cleared the fractions in
Step 1.
• The expression under the radical sign in the quadratic
formula (b2 – 4ac) is called the discriminant.
• The discriminant will take on a value that is positive,
0, or negative.
• The value of the discriminant indicates:
• two distinct real solutions (if it’s positive),
• one real solution (if it’s zero),
or
• two complex but not real solutions (if it’s
negative; this type is discussed further in Math
120).
The discriminant and the kinds of solutions to
ax2 + bx +c = 0
Discriminant
b2 – 4ac
Kinds of solutions
to ax2 + bx + c = 0
b2 – 4ac > 0
Two unequal real solutions
(If b2 – 4ac is a perfect square,
the two solutions will be
rational numbers. If not, they’re
both irrational.)
b2 – 4ac = 0
Graph of
y = ax2 + bx + c
Two x-intercepts
One real solution
(a repeated solution)
(If b2 – 4ac is a perfect square,
the solution will be a rational
number. If not, it’s irrational.)
One x-intercept
b2 – 4ac < 0
No real solution;
two complex imaginary
solutions
No x-intercepts
Example
Use the discriminant to determine the number and
type of solutions for the following equation.
5 – 4x + 12x2 = 0
a = 12, b = -4, and c = 5
b2 – 4ac = (-4)2 – 4(12)(5)
= 16 – 240
= -224
Since the discriminant is negative, there are no real
solutions. (The two non-real solutions will be
complex numbers involving the symbol “ i ”.)
Question: What would this graph look like?
Example
Use the discriminant to determine the number
and type of solutions for the following equation.
25x2 - 4 = 0
a = 25, b = 0 (why?) , and c = -4
b2 – 4ac = (0)2 – 4(25)(-4) = 0 – -400 = 400
Since the discriminant is positive, there are two real
solutions.
(You could go on to show that the solutions are 2/5 and -2/5, either
by factoring or using the quadratic formula.)
Example
Use the discriminant to determine the number and
type of solutions for the following equation.
5 – 4x + 12x2 = 0
a = 12, b = -4, and c = 5
b2 – 4ac = (-4)2 – 4(12)(5) = 16 – 24 = -224
Since the discriminant is negative, there are no
real solutions.
NOTE: There will be two COMPLEX solutions that are
not real numbers, i.e. they will contain the imaginary
number i which is the square root of -1.
Example
Use the discriminant to determine the number
and type of solutions for the following equation.
x2 – 8x + 16 = 0
a = 1, b = -8, and c = 16
b2 – 4ac = (-8)2 – 4(1)(16) = 64 – 64 = 0
Since the discriminant is zero, there is one real
solution. (You could go on to show that the solution is 4,
either by factoring or using the quadratic formula.)
Question: What would this graph look like?
REMINDER:
The assignment on today’s material (HW 42) is due at
the start of the next class session.
Lab hours in 203:
Mondays through Thursdays
8:00 a.m. to 7:30 p.m.
Please remember to sign in on the Math 110 clipboard
by the front door of the lab
Please open your laptops and
find Daily Quiz 36.
• A scientific calculator may be used on this quiz.
• You may also use your yellow formula sheet.
• Remember to turn in your answer sheet to the TA
when the quiz time is up.