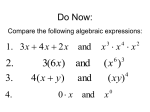Download Monomials, and Negative Exponents

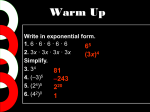
Monomials, and Negative
Exponents
Multiplying and Dividing Monomials
Monomials
A monomial is an expression in algebra that contains one
term, like 3xy.
Monomials include: numbers, whole numbers and variables
that are multiplied together, and variables that are
multiplied together.
Identifying a Monomial
Any number, all by itself, is a monomial, like 5 or 2700.
A monomial can also be a variable, like “m” or “b”. It can
also be a combination of these, like 98b or 78xyz.
It cannot have a fractional or negative exponent. These are
not monomials: 45x+3, 10 - 2a, or 67a - 19b + c.
Two rules about monomials are:
•A monomial multiplied by a monomial is also a monomial.
•A monomial multiplied by a constant is also a monomial.
Multiplying Monomials
Recall that exponents are used to show repeated multiplication.
The power of 3
23 = 2 ∙ 2 ∙ 2
Three factors
Use the definition of an exponent to find the rule for multiplying powers with
the same base.
3 factors
4 factors
23 ∙ 24 = (2 ∙ 2 ∙ 2) ∙ (2 ∙ 2 ∙ 2 ∙ 2) = 27
7 factors
Product of Powers
To multiply powers with the same base, keep the base and
add their exponents
am ∙ an = am+n
32 ∙ 34 = 32+4 = 36
Products of Powers
Examples
53
∙
54
=
57
5 3+4 = 7
(4n3)(2n6) = (4 ∙ 2)(n3 ∙ n6)
Keep the base
Add the exponents
separate the non-exponent factors
from the exponent factor – use the
Commutative and Associative Properties.
= (8)(n3 ∙ n6)
The common base is n
= (8n9)
add the exponents
Dividing Monomials
Recall dividing it the opposite of multiplying
You can also write a rule for finding quotients of powers
26
2∙2∙2∙2∙2∙2
=
22
2∙2 1 1
2∙2∙2∙2∙2∙2
=
2∙2
= 24
1
1
6 factors
2 factors
Divide out the common factors
Quotient of Powers
To divide powers with the same base, keep the base and
subtract their exponents
am
m - n a cannot = 0
=
a
an
45
5 - 2 = 43
=
4
42
Products of Powers
Examples
57
= 54
3
5
57- 3=4
4n9
= (4 ÷ 2)(n9 ÷ n6)
6
2n
Keep the base
Subtract the exponents
separate the non-exponent factors
from the exponent factor
n9
= (2)( 6)
n
The common base is n
= (2n3)
subtract the exponents
Do some examples
Do some examples
Negative Exponents
What Is A Negative Exponent?
8-2
That exponent is negative ... what does it mean?
A Positive exponent meant to multiply.
So Negative? Must be the opposite of multiplying. Dividing!
Dividing is the inverse (opposite) of Multiplying.
HOW?
A negative exponent means how many times to divide by the
number.
Example: 8-1 = 1 ÷ 8 = 1/8 = 0.125
Or
Example: 2-3= 1 ÷ 2 ÷ 2 ÷ 2 = 0.125
Notice that a negative exponents means you divide by 1 and
then divide the base the amount of times as the exponents states.
There a easier way to look at this!
2-3= 1 ÷ 2 ÷ 2 ÷ 2 = 1 ∕8 = 0.125
What did I do?
1st
Calculate the positive exponent
2-3 → 2 ∙ 2 ∙ 2 = 8
Then
Then take the Reciprocal (i.e. 1/an)
=
2-3
1
1
= 3 = = 0.125
2
8
Negative Exponents
Any nonzero number to the negative n power is the
multiplicative inverse of its nth power.
1
= 𝑛
a cannot = 0
𝑎
1
1
-4
5 = 4=
= 0.0016
625
5
a-n
Understanding
Write each expression using
a positive exponent.
Write each expression using
a negative exponent.
1
= 2
6
1
-5
x = 5
𝑥
1
1
= 2 = 3-2
9 3
6-2
5-6 =
p-4
=
1
25
=
1
𝑑5
= d-5
1
16
1
52
=
= 5-2