* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Reconfigurable Computing VHDL
Survey
Document related concepts
Transcript
Reconfigurable Computing Multipliers: Options in Circuit Design
John Morris
Chung-Ang University
The University of Auckland
‘Iolanthe’ at 13 knots on Cockburn Sound, Western Australia
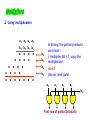
Multipliers
‘Long’ multiplication
x
x x
x x x
x x x
x
x
x
x
x
x
x
x
x
x
x
x
x x
x x
x x
x
x x x
}
multiplicand
In binary, the partial products
multiplier
are trivial –
if multiplier bit = 1, copy the
partial
multiplicand
products
else 0
Use an ‘and’ gate!
product
Multipliers
‘Long’ multiplication
x
a3
b3
x
x
a2
b2
x
x
x x x x
x x x x
x x x x x
a1 a0
b1 b0
x x
x
b0
b1
b2
b3
x
x
In binary, the partial products
are trivial –
if multiplier bit = 1, copy the
multiplicand
else 0
Use an ‘and’ gate!
a3
a2
a1
a0
b0
first row of partial products
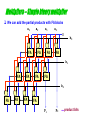
Multipliers – Simple binary multiplier
We can add the partial products with FA blocks
a3
a2
a1
a0
0
FA
FA
FA
b0
FA
b1
FA
FA
FA
FA
b2
FA
FA
FA
FA
p1
p0
product bits
Parallel Array Adder - VHDL
We can build this adder in VHDL with two GENERATE loops
SIGNAL pa, pb, cout : ARRAY( 0 TO n-1 ) OF
ARRAY( 0 TO n-1 ) OF std_logic;
FOR j IN 0 TO n-1 GENERATE -- For each row
FOR j IN 0 TO n-1 GENERATE –- Generate a row
pjk : full_adder PORT MAP( … );
END GENERATE;
This part is straight-forward!
END GENERATE;
… but you need to fill in the PORT MAP
using internal signals!
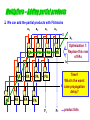
Multipliers – Adding partial products
We can add the partial products with FA blocks
a3
a2
a1
a0
0
FA
FA
FA
FA
b0
Optimization 1:
Replace this row
of FAs
b1
FA
FA
FA
FA
FA
FA
Time?
What’s the worst
b2 case propagation
delay?
FA
FA
p1
p0
product bits
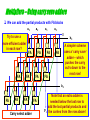
Multipliers – Using carry save adders
We can add the partial products with FA blocks
a3
a2
a1
a0
0
Try to use a
b0
more efficient adder
A simpler scheme
in each row?
uses a ‘carry save’
FA
FA
FA
FA
adder – which
b1
pushes
the carry
out’s down to the
next row!
FA
FA
FA
FA
b2
FA
FA
FA
Carry select adder
FA
Note that an extra adder is
needed below the last row to
add the last partial products and
p0
product
bitsabove!
p1 the carries
from
the row
Multipliers - Tree
Chris Wallace discovered a
way to build fast multipliers
by reducing the number of
carry propagations – and thus
the delay
All the partial product bits can
be generated directly from the
operand bits
A full adder adds 3 input bits
to produce a 2 bit result
Use it to add the bits in
columns
Produce pairs of ‘first level’
sums
Combine bits in these sums
vertically again
······
······
······
······
······
······
······
······
· ··········
·· ·········· ·
···
Combine pp
bits
vertically!
3 at a time
First level
results
Pairs of bits
from FA cells
Multipliers - Tree
Summing the partial products
······
······
······
······
······
······
······
······
· ··········
·· ·········· ·
···
So combine them vertically!
First level results
Signed digit arithmetic – Avoiding the carries!
Terminology
First, we need to distinguish carefully between
digits of a number and
bits used in representing the number
In the standard binary representations,
one bit is used to represent each binary digit (0 or 1) of a number
However, we can use other representation schemes …
If we use more than one bit to represent each digit of an operand, then
we have a redundant system
We’re using more bits than the minimum log2n needed to represent
a number of magnitude, n.
These redundant number systems generally have the ability to
avoid carry propagation
This may be exploited in the addition of sequences of numbers
Carries are transferred to the following addition
Concept similar to that used in carry-save multiplier where carries are
transferred to the following partial product addition
Booth Recoding
A binary number can be re-coded according to Booth’s scheme
to reduce the number of partial products in a multiplier
Original idea
Early computers: shift much faster than add
Observe than when there is a 0 in the multiplier,
you can skip the addition and just shift the multiplicand
In a synchronous computer, this doesn’t help –
in the worst case, you still have to perform an add for each
digit of the multiplier (all or most of them are 1’s)
but
in an asynchronous computer, the ability to skip some
additions reduces the average completion time
Booth observed that when there is a long sequence of 1s,
eg digits j through (down to) k are 1s, then
2j + 2j+1 + … +2k-1 + 2k = 2j+1 – 2k
Booth Recoding
A binary number can be re-coded according to Booth’s scheme
to reduce the number of partial products in a multiplier
Booth recoding
Booth observed that when there is a long sequence of 1s,
eg digits j through (down to) k are 1s, then
2j + 2j+1 + … +2k-1 + 2k = 2j+1 – 2k
Thus the sequence of additions can be replaced by
An addition of the multiplicand shifted by j+1 positions and
A subtraction of the multiplicand shifted by k positions
This is equivalent to recoding the multiplier
from a representation using {0,1}
to one using {-1,0,1} – corresponding to subtract, skip, add
The recoding can be done in O(1) time by inspecting
neighbouring digits
Booth Recoding
Booth’s scheme
Radix-2 Booth recoding
xj
xj-1
yj
Note
0
0
0
No 1’s
0
1
1
End of a string of 1’s - add
1
0
-1
Start of a string of 1’s - subtract
1
1
0
Middle of a string of 1’s - skip
For each position, j,
inspect xj and xj-1 to determine the bits (2 needed!) of yj
Example
x:
1 0 0 1 1 1 0 1 1 0 1 0 1 1 1
y:
-1 0 1 0 0 -1 1 0 -1 1 -1 1 0 0 -1
In practice, this scheme is no use in a synchronous machine,
Worst case: sequence of alternating 0 1
More additions than necessary!
but if we use a higher radix Booth recoding
0 (0)
0
Higher Radix Multiplication
Radix-2 multiplier
Use 1 bit of the multiplier at a time
Form partial product with and gates
Radix-4 multiplier
Use 2 bits of the multiplier at a time
If A is the multiplicand ..
Multiplier
bits
Operation
00
none
01
+A
10
+2A (shift A)
11
+3A (precompute A+2A?)
Radix-4 Booth recoding …
Radix-4 Booth Recoding
Recode multiplier into a signed
digit form
Use 3 bits of the original
multiplier at a time
Recoded multiplier has half
the number of digits,
but each digit is in [-2,2]
Operands to the adders are
now formed by shifts alone
Recode
Constant time
Partial products
Shift, and, select
x2j+1
x2j
x2j-1
yj
Operation
0
0
0
0
No 1’s
0
0
1
1
+A
End of 1’s string
0
1
0
1
+A
Isolated 1
0
1
1
2
+2A
End of 1’s string
1
0
0
-2
-2A
Beginning of 1’s
1
0
1
-1
-A
End one string,
start new one
1
1
0
-1
-A
Start of 1’s string
1
1
1
0
Middle of 1’s
n/2 partial products
generated
Potentially 2× speed!
No carries at all?
Residue Number Systems
Residue Arithmetic
Residue Number Systems
A verse by the Chinese scholar, Sun Tsu, over 1500 years ago
posed this problem
What number has remainders 2, 3 and 2 when divided by the numbers
7, 5 and 3, respectively?
This is probably the first documented use of number
representations using multiple residues
In a residue number system,
a number, x, is represented by the list of its residues (remainders) with
respect to k relatively prime moduli,
mk-1, mk-2, …, m0
Thus x is represented by
(xk-1, xk-2, …, x0)
where
xi = x mod mi
So the puzzle may be re-written
What is the decimal representation of (2,3,2) in RNS(7,5,3)?
Residue Number Systems
The dynamic range of a RNS,
M = mk-1 mk-2 … m0
For example, in the system RNS(8,7,5,3)
M = 8 7 5 3 = 840
Thus we have
RNS(8,7,5,3)
Decimal
(0,0,0,0)
0 or 840 or -840 or …
(1,1,1,1)
1 or 841 or -839 or …
(2,2,2,2)
2 or 842 or …
(0,1,3,2)
8 or 848 or …
Any RNS can be viewed as a weighted representation
In RNS(8,7,5,3), the weights are:
105 120 336 280
Thus (1,2,4,0) represents
(105 1 + 120 2 336 4 + 280 0)840 = (1689)840 = 9
Residue Number Systems - Operations
Complement
To find –x, complement each of the digits with respect to the
modulus for that digit
21 = (5,0,1,0)
so
-21 =
(8-5,0,5-1,0) = (3,0,4,0)
Addition or subtraction is performed on each digit
(
5
,
5
, 0 ,
2
)RNS
(
7
,
6
, 4 ,
2
)RNS
( (5+7)=48, (5+6)=47, 4 , (2+2)=13)RNS
(
4
,
4
, 4 ,
1
)RNS
= 510
= -110
= 410
= 410
Multiplication is also achieved by operations on each digit
(
5
,
5
, 0 ,
2
)RNS = 510
(
7
,
6
, 4 ,
2
)RNS = -110
( (5x7)=38, (5x6)=27, 0 , (2x2)=13)RNS = -510
(
3
,
2
, 0 ,
1
)RNS = -510
Residue Arithmetic - Advantages
Parallel independent
operations on small numbers
of digits
Significant speed ups
Especially for
multiplication!
4 bit x 4 bit multiplier
(moduli up to 15)
much simpler than 16
bit x 16 bit one
Carries are strictly
confined to small
numbers of bits
Each modulus is only a
small number of bits
Can be implemented in Look
Up Tables (LUTs)
6 bit residues (moduli up
to 64)
64 x 64 x 6 bits required
(<4Kbytes)
Residue Arithmetic – Choosing the moduli
Largest modulus determines the overall speed –
Try to make it as small as possible
Simple strategy
Choose sequence of prime numbers until the dynamic range, M,
becomes large enough
eg Application requires a range of at least 105, ie M 105
For RNS(13,11,7,5,3,2), M = 30,300
Range is too low, so add one more modulus:
RNS(17,13,11,7,5,3,2), M = 510,510
Now
• each modulus requires a separate circuit and
• our range is now ~5 times as large as needed, so remove 5:
RNS(17,13,11,7,3,2), M = 102,102
Six residues, requiring
5 + 4 + 4 + 3 + 2 + 1 = 19 bits
The largest modulus (17 requiring 5 bits) determines the speed,
so …
Residue Arithmetic – Choosing the moduli
Application requires a range of at least 105, ie M 105
…
RNS(17,13,11,7,3,2), M = 102,102
Six residues, requiring
5 + 4 + 4 + 3 + 2 + 1 = 19 bits
The largest modulus (17 requiring 5 bits) determines the speed,
so combine some of the smaller moduli
(Remember the requirement is that they be relatively prime!)
Try to produce the largest modulus using only 5 bits –
Pair 2 and 13, 3 and 7
RNS(26,21,17, 11), M = 102,102
Four residues, requiring
5 + 5 + 5 + 4 = 19 bits
(no improvement in total bit count, but 2 fewer ALUs!)
Better …?
Residue Arithmetic – Choosing the moduli
Application requires a range of at least 105, ie M 105
…
RNS(26,21,17, 11), M = 102,102
Four residues, requiring
5 + 5 + 5 + 4 = 19 bits
(no improvement in total bit count, but 2 fewer ALUs!)
Include powers of smaller primes before primes,
starting with
RNS(3,2), M = 6
Note that 22 is smaller than the next prime, 5, so move to
RNS(22,3), M = 12
(trying to minimize the size of the largest modulus)
After including 5 and 7, note that 23 and 32 are smaller than 11:
RNS(32,23,7,5), M = 2,520
Add 11 RNS(11,32,23,7,5), M = 27,720
Add 13 RNS(13,11,32,23,7,5), M = 360,360
Residue Arithmetic – Choosing the moduli
Application requires a range of at least 105, ie M 105
…
Add 13 RNS(13,11,32,23,7,5), M = 360,360
M is now 3 larger than needed,
so replace 9 with 3, then combine 5 and 3
RNS(15,13,11,23,7), M = 360,360
5 moduli,
4 + 4 + 4 + 3 + 3 = 18 bits,
largest modulus has 4 bits
You can actually do somewhat better than this!
Reference:
B. Parhami, Computer Arithmetic: Algorithms and Hardware
Designs, Oxford University Press, 2000
Residue Numbers - Conversion
Inputs and outputs will invariably be in standard binary or
decimal representations,
conversion to and from them is required
Conversion from binary | decimal to RNS
Problem: Given a number, y, find its residues wrt moduli, mi
Divisions would be too time-consuming!
Use this equality:
(yk-1yk-2…y1y0)2mi
= 2k-1yk-1 mi + … + 2y1 mi + y0 mi mi
So we only need to precompute the residues 2 j mi for
each of the moduli, mi, used by the RNS
Residue Numbers - Conversion
For RNS(8,7,5,3) :
• <y>8 is trivially calculated (3 LSB bits)
• For 7, 5 and 3, we need the powers of 2 modulus 7, 5 and 3
j
2j
2 j7
2 j5
2 j3
0
1
1
1
1
1
2
2
2
2
2
4
4
4
1
3
8
1
3
2
4
16
2
1
1
5
32
4
2
2
6
64
1
4
1
7
128
2
3
2
8
256
4
1
1
9
512
1
2
2
Residue Numbers - Conversion
Find 16410 = 1010 01002 = 27 + 25 + 22 in RNS(8,7,5,3) :
• <164>8 is 1002 = 410
j
2j
2 j7
2 j5
2 j3
0
1
1
1
1
1
2
2
2
2
2
4
4
4
1
3
8
1
3
2
4
16
2
1
1
5
32
4
2
2
6
64
1
4
1
7
128
2
3
2
8
256
4
1
1
9
512
1
2
2
<164>7
= <2 + 4 + 4>7
= <10>7
= 3
Note that the
additions are done
in a modular adder!
Worst case:
k additions for each
residue for a k -bit
number
Residue Numbers - Conversion
Conversion from RNS to binary
Digits of an RNS representation can be shown to have position
weightings, eg for RNS(8,7,5,3) the weightings are
105 120 336 280
The weightings may be calculated using the Chinese Remainder
Theorem
x = (xk-1xk-2 … x1x0)RNS = S Mi aixim M
i
where
Mi = M / mi and
ai = < Mi-1>m is the multiplicative inverse of Mi wrt mi
i
This means that
(x3, x2, x1, x0)RNS = x3 × 105 + x2 × 120 + x1 × 336 + x0 × 280
Residue Numbers - Conversion
Conversion from RNS to binary
Digits of an RNS representation can be shown to have position
weightings, eg for RNS(8,7,5,3) the weightings are
105 120 336 280
Calculate position weights with CRT …
This means that
(x3, x2, x1, x0)RNS = x3 × 105 + x2 × 120 + x1 × 336 + x0 × 280
This is most efficiently done through a LUT
Note that the table for RNS(8,7,5,3) requires only
8 + 7 + 5 + 3 = 23
entries
In general, this requires only
Sk-1i=0 mi
words – a reasonable number!
Residue Arithmetic - Disadvantages
Range is limited
Division is hard!
Comparison <, >, sign (<0?) are hard
Still suitable for some DSP applications
Only use +, x
Range is limited
Result range is known
Examples: digital filters, Fourier transforms