* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download 1.4: Functions - Tacoma Public Schools
Large numbers wikipedia , lookup
Functional decomposition wikipedia , lookup
Abuse of notation wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
Continuous function wikipedia , lookup
Principia Mathematica wikipedia , lookup
Non-standard calculus wikipedia , lookup
Dirac delta function wikipedia , lookup
Big O notation wikipedia , lookup
Multiple integral wikipedia , lookup
History of the function concept wikipedia , lookup
Elementary mathematics wikipedia , lookup
Objectives:
1. To determine if a
relation is a function
2. To find the domain
and range of a
function
3. To evaluate
functions
• As a class, use your
vast mathematical
knowledge to define
each of these words
without the aid of
your textbook.
Relation
Function
Input
Output
Domain
Range
Set-Builder
Notation
Interval Notation
Function
Notation
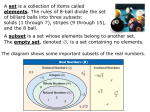
A mathematical relation is the pairing up
(mapping) of inputs and outputs.
A mathematical relation is the pairing up
(mapping) of inputs and outputs.
• Domain: the set of all input values
• Range: the set of all output values
A toaster is an example of a function. You put in
bread, the toaster performs a toasting
function, and out pops toasted bread.
“What comes out of a toaster?”
“It depends on what you put in.”
– You can’t input bread and expect a waffle!
A function is a relation
in which each input
has exactly one
output.
• A function is a
dependent relation
• Output depends on
the input
Relations
Functions
A function is a relation
in which each input
has exactly one
output.
• Each output does not
necessarily have only
one input
Relations
Functions
If you think of the
inputs as boys and
the output as girls,
then a function
occurs when each
boy has only one
girlfriend. Otherwise
the boy gets in BIG
trouble.
Darth Vadar as a “Procurer.”
Tell whether or not each table represents a
function. Give the domain and range of each
relationship.
The size of a set is called its cardinality. What
must be true about the cardinalities of the
domain and range of any function?
Which sets of ordered pairs represent functions?
1. {(1, 2), (2, 3), (3, 4), (3, 5), (5, 6)}
2. {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5)}
3. {(1, 1), (2, 1), (3, 1), (4, 1), (5, 1)}
4. {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5)}
Which of the
following
graphs
represent
functions?
What is an
easy way to
tell that
each input
has only one
output?
A relation is a function iff no vertical line
intersects the graph of the relation at more
than one point
If it does, then
an input
has more
than one
output.
Function
Not a Function
To determine if an equation represents a
function, try solving the thing for y.
• Make sure that there is only one value of y for
every value of x.
Determine whether each equation represents y
as a function of x.
1. x2 +2y = 4
2. (x + 3)2 + (y – 5)2 = 36
Since the domain or range of a function is often
an infinite set of values, it is often convenient
to represent your answers in set-builder
notation.
Examples:
• {x | x < -2} reads “the set of all x such that x is
less than negative 2”.
Since the domain or range of a function is often
an infinite set of values, it is often convenient
to represent your answers in set-builder
notation.
Examples:
• {x : x < -2} reads “the set of all x such that x is
less than negative 2”.
Another way to describe an infinite set of
numbers is with interval notation.
• Parenthesis indicate that first or last number
is not in the set:
– Example: (-, -2) means the same thing as x < -2
– Neither the negative infinity or the negative 2 are
included in the interval
– Always write the smaller number, bigger number
Another way to describe an infinite set of
numbers is with interval notation.
• Brackets indicate that first or last number is in
the set:
– Example: (-, -2] means the same thing as x -2
– Infinity (positive or negative) never gets a bracket
– Always write the smaller number, bigger number
• Domain: All xvalues (L → R)
– {x: -∞ < x < ∞}
• Range: All yvalues (D ↑ U)
– {y: y ≥ -4}
Range:
Greater
than or
equal to -4
Domain: All real numbers
Determine the domain and range of each
function.
• Domain: What you are allowed to plug in for
x.
– Easier to ask what you can’t plug in for x.
– Limited by division by zero or negative even roots
– Can be explicit or implied
• Range: What you can get out for y using the
domain.
– Easier to ask what you can’t get for y.
Determine the domain of each function.
1. y = x2 + 2
1
2. y 2
x 9
Determine the domain of each function.
1. y x 2
2
y
x
2
2.
Functions can also be thought of as dependent
relationships. In a function, the value of the
output depends on the value of the input.
• Independent quantity: Input values, x-values,
domain
• Dependent quantity: Output value, which
depends on the input value, y-values, range
The number of pretzels, p, that can be packaged
in a box with a volume of V cubic units is given
by the equation p = 45V + 10. In this
relationship, which is the dependent variable?
In an equation, the dependent variable is usually
represented as f (x).
• Read “f of x”
–
–
–
–
f = name of function; x = independent variable
Takes place of y: y = f (x)
f (x) does NOT mean multiplication!
f (3) means “the function evaluated at 3” where
you plug 3 in for x.
Evaluate each function when x = -3.
1. f (x) = -2x3 + 5
2. g (x) = 12 – 8x
Let g(x) = -x2 + 4x + 1. Find each function value.
1. g(2)
2. g(t)
3. g(t + 2)
Objectives:
1. To determine if a
relation is a function
2. To find the domain
and range of a
function
3. To evaluate
functions
Assignment:
Continue
Pgs 118-119
#47-79 odd