* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download USING FINITE DIFFERENCES TO WRITE A FUNCTION
Law of large numbers wikipedia , lookup
Elementary mathematics wikipedia , lookup
Horner's method wikipedia , lookup
Vincent's theorem wikipedia , lookup
System of polynomial equations wikipedia , lookup
Fundamental theorem of algebra wikipedia , lookup
Factorization of polynomials over finite fields wikipedia , lookup
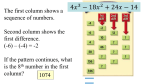
USING FINITE DIFFERENCES TO WRITE A FUNCTION Objective 1.03 Important Definitions Monomial: a number or a product of numbers and variables with whole number expressions. Important Definitions Monomial: a number or a product of numbers and variables with whole number expressions. Example: x 3 Important Definitions Monomial: a number or a product of numbers and variables with whole number expressions. Example: x 3 Polynomial: a monomial or a sum or difference of monomials. Important Definitions Monomial: a number or a product of numbers and variables with whole number expressions. Example: x 3 Polynomial: a monomial or a sum or difference of monomials. Example: 5 x 8 x 3x 3 2 Important Definitions Monomial: a number or a product of numbers and variables with whole number expressions. Example: Polynomial: a monomial or a sum or difference of monomials. Example: x 3 5 x 8 x 3x 3 2 What is the degree of this polynomial? Identify the exponent Degree is 3 FINITE DIFFERENCES OF POLYNOMIALS FUNCTION TYPE DEGREE CONSTANT FINITE DIFFERENCE LINEAR 1 FIRST QUADRATIC 2 SECOND CUBIC 3 THIRD QUARTIC 4 FOURTH QUINTIC 5 FIFTH Example The table to the right shows the population of a city from 1950 – 1980. Write a polynomial for the data. X Y 1950 2000 1960 3000 1970 5000 1980 8000 Find Degree Using Finite Differences X Y 1950 2000 1960 3000 1970 5000 1980 8000 Find Degree Using Finite Differences X Y 1950 2000 1000 1960 3000 1970 5000 1980 8000 Find Degree Using Finite Differences X Y 1950 2000 1000 1960 3000 2000 1970 5000 1980 8000 Find Degree Using Finite Differences X Y 1950 2000 1000 1960 3000 2000 1970 5000 3000 1980 8000 Find Degree Using Finite Differences X Y 1950 2000 1000 1960 1000 3000 2000 1970 5000 3000 1980 8000 Find Degree Using Finite Differences X Y 1950 2000 1000 1960 1000 3000 2000 1970 5000 1000 3000 1980 8000 Find Degree Using Finite Differences X Y 1950 2000 1000 1960 1000 3000 2000 1970 5000 1000 3000 1980 8000 What is the degree of our polynomial going to be? How many steps did we take to get to a constant difference? It took us 2 columns of differences to get to 1000. So the degree is 2. Our polynomial will look something like this: What is the degree of our polynomial going to be? How many steps did we take to get to a constant difference? It took us 2 columns of differences to get to 1000. So the degree is 2. Our polynomial will look something like this: __ x ___ x ___ 2 What is the degree of our polynomial going to be? How many steps did we take to get to a constant difference? It took us 2 columns of differences to get to 1000. So the degree is 2. Our polynomial will look something like this: ax bx c 2 Using Graphing Calculator Click Stat Choose Edit Put the x values in List 1 Put the f(x) values in List 2 Click 2nd Click quit Click Stat Choose Calc Choose proper function Quadratic Using Graphing Calculator Click 2nd Click Stat Put the x values in List 1 Put the f(x) values in List 2 Click 2nd Click quit Click Stat Calc Choose proper function Quadratic 5 x 19450 x 18917000 2 Make a Prediction Use your polynomial to tell me what the population will be in the year 2020. Make a Prediction Use your polynomial to tell me what the population will be in the year 2020. 5(2020) 19450(2020) 18917000 2 Make a Prediction Use your polynomial to tell me what the population will be in the year 2020. 5(2020) 19450(2020) 18917000 2 = 30,000 people in 2020 Your Turn! In your groups, use what you have learned to create a polynomial from the given information. Use your polynomial to make the prediction. Pictures Came From http://www.flickr.com/photos/moomoo/2462069317/ http://commons.wikimedia.org/wiki/File:TI-84_Plus.jpeg http://www.flickr.com/photos/64281135@N00/54335576 http://school.discoveryeducation.com/clipart/clip/pyramids.html http://jwilson.coe.uga.edu/emt668/EMAT6680.2004.SU/Bird/emat6690/trapezoid/trapezoid.html http://jwilson.coe.uga.edu/emt668/EMAT6680.2004.SU/Bird/emat6690/trapezoid/trapezoid.html http://www.free-clipart-of.com/FreeBasketballClipart.html Works Cited Burger, E.B., Chard, D.J., Hall, E.J., Kennedy, P.A., Leinwand, S.J., Renfro, F.L., Seymour, D.G., & Waits, B.K. (2011). Algebra 2 (teachers edition). Orlando: Houghton Mifflin Publishing Company.